相机模型
      简单的说，摄像机成像过程的实质是4个坐标系的转换，首先，空间中的一点由世界坐标系转换到相机坐标系，此时的点仍处于空间；然后将空间的点投影到成像平面上，完成相机坐标系转换到图像物理坐标系，此时的点已经投影到成像平面，是个二维点；最后成像平面上的点转换成图像平面，此时点参考的坐标系变为图像像素坐标系。

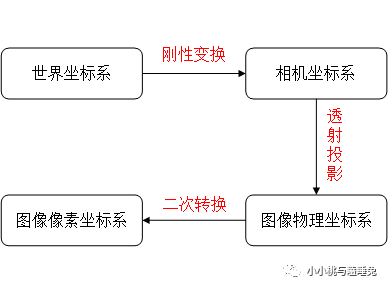
      我们可以看最简单的相机模型：针孔模型，针孔模型，如下图，f是相机焦距，Z是相机到物体的距离，X是物体的长度，x是图像平面上的物体图像。根据相似三角形可以得到公式：


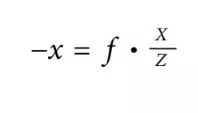
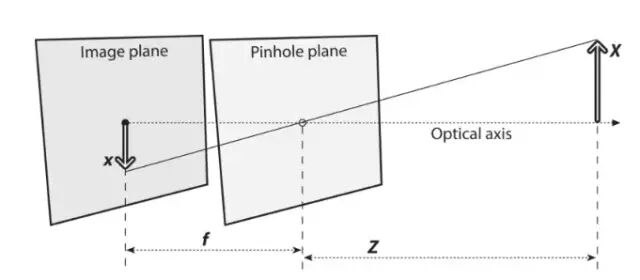
      对上述针孔模型作等价转换，交换针孔和图像平面，原本针孔介于物体和物体图像之间，图像里物体是倒立的（故上式带负号），现在物体图像介于针孔和物体之间，此时针孔中的点被理解为投影中心，这样，每一条光线从远处物体的某个点出发，到达投影中心，与新图像平面相交的点就是投影点。光轴与图像平面的交点被称为主点。值得注意的是，转换后的针孔模型是其数学形式更加简单，但这种典型的数学抽象无法在物理上构建。此时的公式为上式去掉负号。
      
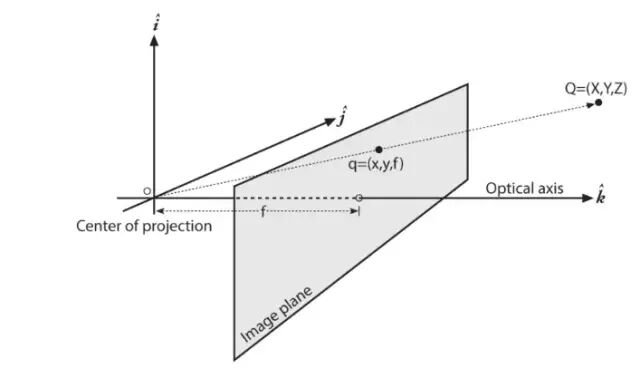
     由于工艺的限制，成像装置很难做到主点在中心位置（拿着镊子和胶水以微米级别的精度安装或许可以实现），因此，芯片的中心通常不在光轴上。我们对投影屏幕坐标中心可能的偏移（对光轴而言）进行建模，即物理世界的点Q，其坐标为（X, Y, Z），投射到成像装置上的某个像素点，有：

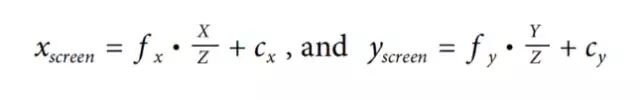
其中，cx、cy是坐标中心偏移引入的两个新参数，fx、fy是引入的两个不同的焦距，此处焦距fx实际上是透镜的物理焦距长度与成像装置每个单元尺寸Sx的乘积（Sx的单位为像素/每毫米，f的单位是毫米），这样做的目的是，Sx、Sy以及物理焦距 f 均不能在相机标定过程中直接测量，只有组合量fx = f * Sx，fy = f * Sy 可以直接计算出来，避免拆除相机去直接测量其部件。求得的（xscreen, yscreen）是像素坐标。
射影几何基础
      将物理世界中坐标为（X, Y, Z）的一系列物理点Q映射到投影平面上坐标为（x, y）的点的过程叫射影变换。采用这种变换一般要使用齐次坐标。
齐次坐标：齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示（例如：x, y, z 变成x, y, z, w），其额外限制是任意两个点的值成比例时即为等价点。
      用一个三维向量q = (q1, q2, q3)来表示平面上的点，由于所有点在投影空间中的比例值是相同的，因此我们可以通过除以q3得到实际的像素坐标值。这样一来，便允许我们将定义相机的参数（如fx, fy, cx, cy）重新排列为一个3 * 3的矩阵，称为相机的内参矩阵。
      将物理世界中的点投影到相机上，可以用下式简单表示：


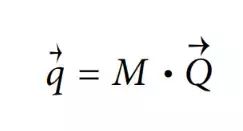
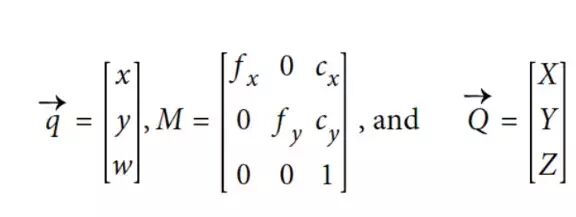
10.22
参考： 
learning opencv3 
https://www.jianshu.com/p/887dd060ea99