
什么是数学思维?
用数学的观点去思考问题和解决问题的能力?
用数学课标中的定义,数学思维能力,指:会观察、实验、比较、猜想、分析、综合、抽象和概括;会用归纳、演绎和类比进行推理;会合乎逻辑地、准确地阐述自己的思想和观点;能运用数学概念、思想和方法,辨明数学关系,形成良好的思维品质。
我们都希望,我们的孩子,能拥有牛顿般的数学思维,让大自然像一本打开的书一样展现在孩子的面前。那如何才能做到呢?
看我们来自上海交通大学数学与应用数学学士、工商管理学士,新加坡南洋理工大学数学博士,新加坡沈基文金融研究所博士后,新加坡科技研究局科学家,贾博士如何为我们深入浅出的展现出来。
1.勾股定律

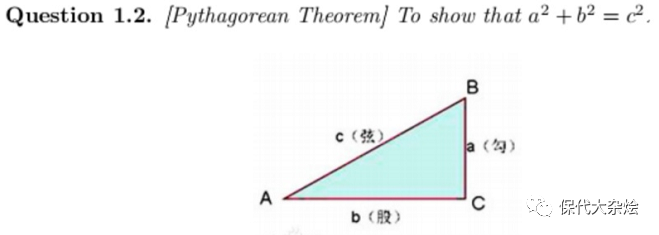
大家还记得a^2+b^2=c^2是如何证明的么?
直角三角形,边长为a,b,c
b边延长长度a,做直角边长度为b,再延长长度a,再做直角,并延长这条直角边。
三角形短边a的边,延长,与上述最后延长的直线相交。形成如下图所示。
由于前3个角都为直角,因此最后相交的角也为直角。
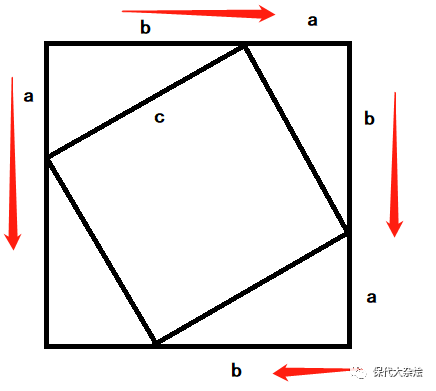
得到这个图,我们似乎很理所当然的就看到大正方形的面积等于四个小三角形面积加上中间边长为c的小正方形面积,即:
(a+b)^2 = 4 * 1/2 * a * b + c^2
a^2+2ab+b^2=2ab+c^2
从而得到:a^2+b^2=c^2
但,凭什么你确定最后一个三角形就是边长为a,b,c的直角三角形呢?
凭什么中间就是边长的c的正方形呢?
最后一个三角形,在作图的时候只能确定是两条直线相交。至于边长是需要证明的。
这点证明不难,可以用相似三角形来证明。
同理可证明内部为边长为c的小正方形。
至此,勾股定律即可完整证明。
总结:虽然有时候一眼看过去感觉像,也不能想当然的认为就是,数学是严谨的,证明要从最基础的小处开始,多问一个为什么,凭什么。将具体的特例抽象成广泛适用的公式,就是数学最有趣的地方了。
2.九宫格填数
题:将1到9这九个数字填写入下图的九宫格中,要求任一横排、竖排、斜排三个数相加之和相等。

可能不少家长,尤其是学过奥数的家长和学生,都知道这道题,并且知道它的做题技巧。
填写方法:从右上的方格到左下的方格斜着按数字大小填写,九宫格中已填的数字就不用再去动它了,我们只需要把增设的方格内的数字填回到九宫格中就可以了。方法为:将增设方格内的数字填写到它对面(不是相邻)的空格内,详见下图。

确实,只要记住上述的窍门,工具,我们就可以很快的解出这道题。但是,为什么呢?为什么会有这样的方法?
在不考虑任何方法的情况下,这道题要怎么做呢?
1到9,全部加起来等于45,每行或每列和都要相等,即这个和必然为45/3=15
由此,需要3个不重复的数相加等于15,有多少中可能呢?
用穷举法,从1开始,加的第二个数逐渐变大,直到重复为止。
1+5+9=15;1+6+8=15;
2+4+9=15;2+5+8=15;2+6+7=15
3+4+8=15;3+5+7=15
4+5+6=15
穷举下来我们发现,也就8组不重复的数相加和为15
由于九宫格中横纵斜相加,中间的数字要用4次,从8组数中可以看到只有5出现了4次,将5放入其中,对称的放入其他数字即可。
穷举法虽然底层逻辑简单,但未免耗时。
我们可以观察,1-9中,5是中间数,九宫格中,最中间的是与其他格都无对称关系的为止,因此最中间的格放5最合适。剩下的1和9,2和8……依次搭配。但第一步填的1和9,应该在四角位置还是中间位置呢?考虑3条边的和为15,奇数。即3条边的3个数字必须有奇数个奇数,即1个奇数或3个奇数。由于一共就5个奇数,因此只能妥协为最外层的横竖边上只有1个奇数,即四角的数为偶数,随手填进去即得到:

再将对应的另外两个奇数3和7填到横向的两格中,由于对称关系,1和9谁在上谁在下,3和7谁在左谁在右并不重要。

剩下的2,4,6,8。2和8一组,4和6一组,大小搭配,7,8,9三个较大的数,横竖不相遇,因此未填的8只能在右上角位置,对应的2落右下,对应的4与6的位置也就确定了:



简便方法或公式,都是前人总结出来的经验工具,但我们不能只有经验工具,如果只学会用一种工具应对一种题型,那不叫数学思维,那叫工具应用。数学思维是大胆假设和小心求证,是仔细观察,逐步尝试。一如最出名的小学生柯南所说:“当排出了所有其它的可能性,还剩一个时,不管有多么的不可能,那都是真相 ”
3.整除问题
题:2019n是9的倍数,n为多少?
解:2+0+1+9+n=12+n,由于被9整除需要各位数字之和可以被9整除,所以n为6. 即20196为9的倍数。
如果你不知道这个技巧,这道题要怎么办?
方法1,假设n=0,用20190除以9得到的余数为3,为能整除,各位补6即可
方法2,2019n,先减个9的倍数18000得219n,再减个9的倍数1800得39n,再减9的倍数360得3n,根据乘法口诀,n为6
学过速算的都知道,只要各位数字之和能被9整除,那这个数就能被9整除。
没错,那我们再往深的问一层:那这个技巧又是如何来的呢?
2019n为特定数字,为了证明工具的代表性,假设数字为abcde
即abcde=a*10000+b*1000+c*100+d*10+e
a0000/9=9999*a+a
b000/9=999*b+b
c00/9=99*c+c
d0/9=9*d+d
e/9=0*9+e
由此可知,只要a+b+c+d+e的和能被9整除,abcde这个数就可以被9整除。
延伸一下,整除为余数为0的状态,换句话说想要某个书除以9余几,只要这个数各位上的数的和除以9余几就可以了。
作为老师,为了成绩,可能需要学生尽快掌握工具来应对考试。然而对于我们家长,我们应该帮助孩子,在工具的基础上进一步,再进一步,多提几个为什么,凭什么,让我们的孩子从缺乏基础的的空中楼阁工具性思维中,转变为基础扎实,有理有据,可千变万化的数学思维中。
