The Drunkards Walk：How Randomness Rules Our Lives

（续前）
第六章 假阳性与好错误
 
许多阴谋论都源于对这个逻辑关系的错误理解，也就是说，当一系列事件是巨大阴谋的产物时，这些事件发生的可能性，与当一系列事件已经发生时，这些事件证明存在着巨大阴谋的可能性，两者被混为一谈了。贝叶斯理论所讨论的全部内容，就是当其他事件已经发生，或说给定其他事件发生的前提下，对于某事件发生的可能性所造成的影响。
 
我们转到与第三章中的两个女儿问题相关的另一个问题上来。设想一个远房表亲有两个孩子。回想一下，在两个女儿问题中，我们知道这两个孩子中有一个或两个是女孩，而我们要搞清的，则是到底有几个女孩，一个还是两个？如果一个家庭中有两个孩子，那么如果其中至少有一个是女孩的话，两个都是女孩的可能性为多大？
 
但“如果”两字，将问题变为了一个条件概率问题。如果没有这个“如果”，两个孩子都是女孩的可能性是1/4，对应的4种可能的出生顺序为（男孩，男孩）、（男孩，女孩）、（女孩，男孩）和（女孩，女孩）。但知道至少有一个是女孩的这个额外信息时，两个都是女孩的可能性就变为了1/3，这是因为如果至少一个孩子是女孩的话，那么两个孩子的性别就只有3种可能情况——（男孩，女孩）、（女孩，男孩）和（女孩，女孩），其中1种正好对应了两个孩子都是女孩的结果。这也许就是理解贝叶斯思想的最简单方法——首先，把样本空间——也就是所有可能情况的清单——写下来，如果这些情况的可能性不等，就将其各自的概率也一同记下。接着，把被条件（在现在的问题中，就是“至少有一个女孩”这个条件）所否定掉的那些可能性划掉，剩下的就是条件满足时的可能情况，以及它们的相对概率。

这个方法看来似乎理所当然。自信爆棚的你也许会觉得，不用亲爱的贝叶斯神父来帮忙，自己也能想通这一点，于是这个变体如下：某家庭有两个孩子，如果两个孩子之一是名叫佛罗里达的女孩，那么两个孩子都是女孩的概率有多大？是的，我说的是一个名叫佛罗里达的女孩。实际上，佛罗里达是20世纪最初30年左右的时间中，1000个最常见的美国女性名字之一。我很仔细地挑出这个名字，因为现在的谜题，部分就在于佛罗里达这个名字的什么东西——如果真有某个东西的话——影响了我们感兴趣的概率？
 
在继续之前，请思索一下这个问题：在这个“名叫佛罗里达的女孩”问题中，两个都是女孩的可能性，是否仍为1/3（就如两个女儿问题的答案一样）？
 
我很快就会证明，这个答案是“否”。有一个女孩名叫佛罗里达的事实，将我们所寻找的概率变成了1/2：如果你想不通，也不必忧虑。理解随机性乃至所有数学问题的关键，并不在于能仅靠直觉就立刻知道问题的答案，而在于掌握能求得答案的工具。
 
伯努利定理关心的是，假如你打算用一枚平衡的硬币进行多次投掷，那么可以期望得到的正面朝上的次数是多少，而贝叶斯研究的却是伯努利最初的目标，即当你得到了正面朝上的次数时，你能在多大程度上信任硬币的平衡性。
 
使贝叶斯留名至今的理论，在1763年12月23日而最初为人所知。这篇由贝叶斯撰写的论文名为《通往机遇学说的一个问题之解决的短文》，并于1764年发表在皇家学院的《哲学汇刊》（Philosophical Transactions）上。如我所述，贝叶斯是在试图回答那个激发了伯努利的相同问题时，发展出条件概率的：我们如何才能根据观察来推出其后隐含的概率？如果一种药物在临床试验中仅仅治愈了60名病人中的45名，那么对于药物在下一个病人身上有效的可能性，这个数据所能告诉我们些什么？如果药物是对100万名病人中的60万名有效，那么其有效率落在60%附近的可能性显然很高。但当结果是来自规模更小的试验时，从中能得出什么结论呢？贝叶斯同时还问了另一个问题：如果在试验之前有理由相信该药物的有效率只有50%，那么今后评估有效率时，试验所得的新数据应占有多大的权重呢？我们大多数的生活经验都类似于此：观察一个相对较小的结果样本集，由此获得若干信息，然后对产生出这些结果的内在性质加以判断。但这一系列推理应当如何进行呢？
 
贝叶斯是通过一个类比来考虑的。设想有人提供了一张方桌和两个球。我们将第一个球滚落在桌子上，并且使它以等可能性停止在桌上的任意一点。我们现在要做的，是在看不到桌子和球的情况下，确定这个球停止在由左至右的坐标轴上的哪一点，而使用的工具就是那第二个球。我们以相同的方式反复将第二个球在桌上滚动，同时，一名合作者将观察第二个球的停止位置，是在第一个球的左边还是右边，并把这个结果记录下来。试验结束后，合作者将会把第二个球落在两个大范围内的次数分别告诉我们。第一个球即对应我们希望获得的未知量，第二个球代表的则是我们能够得到的证据。如果第二个球都停在了第一个球的右边，我们就可以很有把握地认为，第一个球停在了离桌子最左边很近的地方；如果第二个球并非如此一贯地停在这个范围内，那么我们对于上述结论的信心也相应降低，或者去猜想第一个球实际落在了比我们假设的位置更靠右的地方。贝叶斯所表明的，就是如何根据第二个球的数据，来确定第一个球落在左-右坐标轴上任意给定位置处的准确概率，以及在给定附加数据的情况下，如何去修正概率的初始估计。按贝叶斯的术语，初始估计称为先验概率，而修正后的新猜测称为后验概率。
 
贝叶斯之所以设计出这个游戏，是因为它可以对应生活中的许多决策。在药物试验的例子中，第一个球的位置代表了药物的真实有效率，而第二个球所提供的，则相当于在病人身上得到的试验数据。第一个球的位置同样还能代表一部影片的受欢迎与否、产品质量、驾驶技术、勤奋与否、固执与否、天分高低、能力高低或任何能决定事情成败的东西。而第二个球所提供的东西，就代表了我们的观察或收集得到的数据。贝叶斯理论所说明的，就是如何估计未知概率，然后根据新的数据来对其加以修正。如今，贝叶斯分析已广泛应用于科学和产业的各个领域。
 
假设你申请保险时的驾驶记录表明，过去20年中你一次事故也没有发生，或是在这20年中，你碰到了37次事故，那么保险公司将很清楚应该把你归入哪一种类型。但如果你是一名新手，那应该把你放在低危类型呢，还是高危类型。由于公司并没有你的个人数据——或说对“第一个球的位置”完全一无所知——它也许会以相等的先验概率将你归入任何一类之中，或者根据新司机的一般性数据，来估计你属于高危类型的初始可能性为（比方说）1/3。后一种情况下，公司可能会将你作为一个杂合体来建模——即1/3的高危加2/3的低危——并按1/3的高危保险费加2/3的低危保险费来收钱。经过一年的观察——也就是贝叶斯那第二个球被滚动一次后公司就会使用新的数据来重新评价模型，调整之前所设的1/3和2/3的比例，再重新计算出应该收取的保费。如果这一年中你没有发生事故，那么低危的比例以及对应的低费用的比例就会相应增加；而如果发生了两次事故的话，那么这些比例就会相应降低。精确的调整幅度由贝叶斯定理给出。按同样的方式，保险公司今后就能周期性地调整评估值，以便反映出你到底是无事故类型的驾驶员，还是那个一连两次都因为在单行道上开错方向、左手拿着手机、右手还拿着甜面包圈而造成事故的家伙。这也就是保险公司给“好司机”打折的原因：无交通事故实际上提升了一名司机属于低危类型的后验概率。
 
显然，贝叶斯定理的许多细节都十分复杂。
 
关键在于利用新的信息去“裁剪”样本空间，并相应调整各个概率。在两个女儿问题中，初始样本空间为（男孩，男孩）、（男孩，女孩）、（女孩，男孩）和（女孩，女孩）；但如果我们得知至少有一个是女孩，样本空间就缩减为（男孩，女孩）、（女孩，男孩）和（女孩，女孩），从而使两个都为女孩的可能性变为了1/3。让我们使用这个简单策略，来看看当有一个孩子是名为佛罗里达的女孩时，会发生些什么。在名叫佛罗里达的女孩问题中，新信息不仅与孩子的性别有关，而且还与女孩的名字有关。既然初始样本空间是一张所有可能情况的清单，那在现在的例子中，它就是一张包括了性别与姓名的清单。我们以女孩F来表示“名叫佛罗里达的女孩”，以女孩NF来表示“名字不是佛罗里达的女孩”。于是样本空间写下来就是这么个样子：（男孩，男孩）、（男孩，女孩F）、（男孩，女孩NF）、（女孩F，男孩）、（女孩NF，男孩）、（女孩NF，女孩F）、（女孩F，女孩NF）、（女孩NF，女孩NF）和（女孩F，女孩F）。现在我们来裁剪样本空间。既然已知两个孩子之一是名为佛罗里达的女孩，故样本空间可以缩小为（男孩，女孩F）、（女孩F，男孩）、（女孩NF，女孩F）、（女孩F，女孩NF）和（女孩F，女孩F）。至此，现在的问题就与原先的两个女儿问题有所不同了。由于一个女孩叫或不叫佛罗里达的概率并不相等，因此，这个样本空间中的元素并非是等概率事件。
 
即使不考虑父母通常都不会给孩子们起重名的这个事实，两个女孩都叫佛罗里达的可能性也仍然微乎其微，因此我们完全可以忽略掉两个女孩都叫佛罗里达的可能性，而剩下的样本空间中，就只剩下（男孩，女孩F）、（女孩F，男孩）、（女孩NF，女孩F）和（女孩F，女孩NF），而它们十分近似于等概率事件。既然在4个元素中有2个——或者说有一半——对应了这一家子有两个女儿的情况，因此问题的答案就不再如两个女儿问题那样是1/3，而变成了1/2。这个增加的信息——关于女孩姓名的知识——造成了答案的不同。
 
这个例子中的内在关系十分简单，而同样的推理可以使许多生活中的真实局面变得更加清晰明了。下面，我们就来说几个这样的实际情况。
 
我与贝叶斯神父最值得记住的遭遇，发生在1989年某个周五的下午。当时，医生打电话告诉我，我将有999/1000的可能性在10年内死去。他补充道：“我真的十分抱歉。”很难描述甚至是回忆我到底是如何度过那个周末的，不过简单来说，那个周末我可没有去迪斯尼乐园。可为什么有了这个死亡判决，我却还好好地在这里，并写书来谈论它呢？
 
这次历险始于妻子和我申请人寿保险之时。申请中需要进行血检。一两周后，我们的申请被拒了。给我的信中说道，公司由于“你的血检结果”而否决了我的保险申请，而给我妻子的信中则说是由于“你丈夫的血检结果”而拒绝了她的申请。
 
我带着不祥的预感去看了医生，进行了一次HIV检查。检查结果呈阳性。尽管开始时，我因为过于震惊而没有询问这个几率是否真的可靠，但后来我了解到，医生是如下得到那个1/1000的健康概率的：在1000个没有艾滋病毒的血液样本中，有1个的HIV检查结果会呈阳性。这听起来似乎跟他说的是一回事，但事实并非如此。医生将“如果我没有感染HIV而检查结果呈阳性”的概率和“如果我的检查结果呈阳性而我并没有感染HIV”的概率搞混了。
 
为了明白医生的错误，我们来运用一下贝叶斯方法。首先是定义样本空间。我们可以把所有曾接受过HIV检查的人都包括进来，但如果多用一点与我有关的附加信息来定义样本空间，那结果会更准确一些：我们只考虑所有曾接受过HIV检查的、异性恋的、不滥用静脉注射吸毒的美国白人男性。
 
接下来，我们将这些人加以分类。与本问题有关的类型不再是男孩或女孩，而是检查呈阳性且确实为HIV感染者的人（真阳性）、检查呈阳性但没有感染HIV的人（假阳性）、检查呈阴性且没有感染HIV的人（真阴性）以及检查呈阴性但实际感染了HIV的人（假阴性）。
 
最后，让我们问一问，每种类型的人数有多少呢？考虑一个10000人的初始人群。根据疾病控制与防治中心的统计数据可以估计，在1989年，大约每10000名接受检查的异性恋不滥用毒品静脉注射的美国白人男性中，就有1名感染了HIV。假设假阴性率十分接近0，这就意味着，大约每10000人中有1人会因为真实感染而被检测到阳性。此外，由于假阳性率为——如医生所说的——1000分之1，因此，大概另有10人虽然没有感染HIV，但还是被查出为阳性。而样本空间的10000人中剩下的9989人，检查结果将为阴性。
 
现在裁剪样本空间，使之仅包含那些检查结果为阳性的人。这样得到的，就是10个假阳性和1个真阳性，换句话说，在11个被查出为阳性的人中，仅仅只有1个真地感染了HIV。医生告诉我检查结果出错——即我实际上十分健康——的可能性是1/1000，而他真正应该说的是：“不用担心，你没有感染的机会不小于10/11。”就我的情况而言，这个筛检明显是被我血液中的某种标记物所糊弄了，虽然筛查所要发现的病毒其实并不存在。
 
但上面的遭遇表明，已知假阳性率，并不足以确定检查的有用性，还应该将假阳性率与疾病的真实流行情况加以比较才行。如果是十分罕见的疾病，那么即使是低的假阳性率，也不意味着阳性结果就代表了确实患病；而如果是常见疾病，阳性结果就更可能具有意义。现在假设我是同性恋，并被查出阳性，再来看看疾病的真实流行程度对阳性结果诊断意义的影响
 
假定在1989年的男同性恋人群中，那些接受检查的人被感染的可能性为1%左右。这就意味着在10000个检查结果中，我们得到的不是之前的1个、而是100个真阳性，连同10个假阳性。在这种情况下，这个阳性结果将以11分之10的比率，来表明我的确被感染了。确定是否来自于高危人群之所以十分有助于评价检查结果，其原因就在于此。贝叶斯理论表明，B发生时A也将发生的概率，一般不同于A发生时B也将发生的概率。医生这个职业中的一个常见错误，就是未能清楚认识到这一点。比如一些在德国和美国进行的研究中，已知有7%的乳腺 X射线检查在实际没有肿瘤时仍给出阳性结果，
 
研究者们请医师估计一下，一名无症状的、40至50岁且乳腺X射线检查结果为阳性的妇女，她真正患乳腺癌的可能性有多大[8]。此外，这些医生们还被告知，实际的乳腺癌发病率约为0.8%，而真实的假阳性率约为10%。把所有这些数据凑拢来，利用贝叶斯方法就能得出：真正因癌症而导致的乳腺X线检查阳性结果的比例，仅仅只有9%左右。但在德国医生组中，有1/3的医生认为这个概率为90%，而所有估计值的中值为70%。在美国医生组中，100名医生中就有95名估计这个概率应该在75%上下。
 
在法律圈中，有时将与上述相反的错误称为“检控官谬误”，因为检察官们常常使用这种靠不住的论断，来诱导陪审团根据单薄的证据对疑犯定罪。
 
英国的莎莉·克拉克案（Sally Clark）[10]。克拉克的第一个孩子于出生后11周死亡。据称其死亡原因是婴儿粹死综合征（Sudden Infant Death Syndrome，SIDS）——当婴儿意外死亡而尸检又无法查出致死原因时所做出的诊断。克拉克再次怀孕，而这次她的孩子在第8周时死亡，死因再次被认为是SIDS。事情发生后，克拉克被捕并被指控将两个孩子窒息致死。在法庭上，检方传唤了资历颇深的儿科医生罗伊·梅道（Roy Meadow）爵士来证明，由于SIDS的罕见性，两名婴儿都死于SIDS的可能性只有7300万分之1。除此之外，检方没有拿出任何不利于被告的实质证据。那么，这个几率是否足以对克拉克定罪呢？陪审团觉得够了。因此，1999年11月，克拉克太太入狱服刑。
 
梅道爵士估计的是一名婴儿死于SIDS的机会：1/8543。既然现在有两个孩子，那么他们都死于SIDS的几率，就是把上面这个数字跟自己再乘一次，从而得到了7300万分之1。不过这个计算隐含的假设，是两起死亡事件相互独立——也就是说，即使在哥哥或姐姐死于SIDS的情况下，也没有任何环境或遗传因素会增加第二个孩子的死亡风险。但实际上，在审判结束数周后出版的《英国医学杂志》（British Medical Journal）之编者按中，给出两名兄弟姐妹都死于SIDS几率的估计值为275万分之1。这个机会当然还是很小。
 
要理解克拉克之所以是蒙冤入狱的关键，仍在于考虑相反的错误：我们真正要找的，并不是两个孩子都死于SIDS的概率，而是两个孩子的死亡，都是由SIDS所造成的概率。克拉克入狱两年后，皇家统计学会（Royal Statistical Society）通过一份新闻稿加入了这个话题，声明称陪审团的决定是基于“一个严重的、被称为检控官谬误的逻辑错误。陪审团应当衡量的，是对婴儿死因的两种相互对立的解释：SIDS或谋杀。两起死亡都是由于SIDS或谋杀所造成的可能性都十分小，但显然其中之一就发生在本案之中。真正重要的，是造成死亡的相对似然性……而不仅仅是[死于SIDS的情况]到底有多么不可能……”一名数学家后来对一个家庭因为SIDS或谋杀而失去两个孩子的相对似然性作出了估计。根据可得到的数据，他的结论是，两名婴儿是SIDS受害者的可能性，9倍于谋杀致死的可能性。
 
克拉克家因此提起上诉，并且在上诉庭中聘请了统计学家作为专家证人。上诉以败诉告终，但他们仍然继续寻求死因的医学解释，并于此期间发现了一个被隐藏的事实：检方的病理学家隐瞒了第二名婴儿在死前遭遇病菌感染的事实，而这个感染可能会导致其死亡。由于这个发现，法官撤销了有罪判决。在坐了差不多3年半的牢房后，克拉克被释放出狱。著名律师、哈佛大学法学院教授阿兰·德什维兹（Alan Dershowitz）也曾同样成功地运用了检控官谬误——以在审理辛普森（O．J．Simpson）谋杀前妻妮可·布朗·辛普森（Nicole Brown Simpson）及其男性同伴的案件中，为辛普森进行辩护。辛普森这名前橄榄球明星的案子，是1994~1995年的媒体大热点之一。警方掌握了足够的不利证据：他们在其住所发现了一只染血的手套，而且与在谋杀现场发现的那只似乎正好是一对；在两只手套上、辛普森的白色福特Bronco中、卧室中的一双袜子上以及车道和房屋中，都发现了与妮可血型相符的血迹；更进一步地，罪案现场提取到的血样DNA分析结果，与辛普森的DNA相吻合。辩方除了以种族主义——辛普森是一名非裔美国人——指责洛杉矶警察局，并对警方的可靠性以及所提供证据的权威性提出指责之外，大概就帮不上更多的忙了。
 
检方决定在案子开场时，将焦点集中在辛普森对妮可的暴力倾向上。检察官将开庭后最初10天的时间花在了展示被告虐待妻子的证据上，并声称仅仅根据这些证据，就已经有很好的理由怀疑被告谋杀了被害人。。因此辩方称，在那些抽伴侣耳光或殴打伴侣的男人中，没有几个真正发展到了谋杀的地步。这对不对呢？对。确信无疑？是。与本案有关？无关。与本案有关的数字，不是一个殴打妻子的男人会进而杀害她的概率（1/2500），而是一名遭殴打并被谋杀的妻子是被她的施虐者所杀害的概率。根据1993年的美国及其领地犯罪报告汇编，德什维兹（或检方）应当提供的概率是下面这个：1993年，在所有遭谋杀的被虐美国妻子中，差不多有90%是被施虐者所杀害。这个统计数字却没有出现在法庭上。
 
当判决时刻即将到来时，长途电话的通话量掉了一半，纽约股票交易所的交易量则下降了40%。据估计，大概有1亿人打开电视或收音机龄听最终判决：无罪。德什维兹大概对于他误导陪审团的行为问心无愧，因为按他的话说：“法庭宣誓——‘陈述事实、事实之全部以及仅仅事实’——只适用于证人。辩护律师、检察官和法官都不用进行这个宣誓……事实上，可以很公平地说，美国司法系统是建立在不说出全部事实的基础之上。”
 
尽管条件概率是认识随机性的一场革命，贝叶斯本人却一点也不革命。
 
让科学家们注意到贝叶斯的观点，并最终向世界说明如何根据观察结果来推算出隐藏的真实概率，这一重任就落在了另一个人——法国科学家与数学家拉普拉斯（Pierre Simon de Laplace）的肩上。
 
你大概还能记得，在我们实际进行一系列扔硬币试验之前，伯努利的黄金定理能告诉我们观察到某个特定试验结果的可能性——如果硬币是公平的话。你可能也还记得，这个定理并没有告诉我们，在进行了特定某一系列投掷之后，投掷结果能表明硬币是公平的可能性有多大。按同样的思路，如果我们知道一名85岁老人能活到90岁的可能性为50对50，那么黄金定理就能指出，1000名85岁老人组成的群体，其中一半在接下来5年中过世的几率有多大；但如果某个群体中有一半的人在85岁到90岁的年龄段去世，定理却不能告诉我们，这个群体中个体生存率为50对50的可能性有多高。
 
除了与赌博有关的情况之外，我们通常没有关于所需概率的理论知识，因而必须在一系列观察之后对其进行估计。科学家们也发现他们处境相同：他们一般不是在给定了某个物理量的值之后，去得到对该物理量测量的结果是这个或那个的可能性，而是在给定了观测结果后，去试图发现某个物理量的真实值。
 
我着重强调了这两类问题的区别，因为它十分重要。这个区别定义了概率与统计之间最根本的不同：前者关心的是根据确定概率来进行预测，而后者考虑的是根据观测数据来推出那些概率。
 
拉普拉斯阐明的就是后一类问题。在他框架中的问题如下：给定一系列观测值时，我们对被观测量的真实值所能做出的最佳估计是什么？这个最佳估计落在真值“附近”——不管这个附近的定义如何苛刻——的机会是多少？
 
拉普拉斯的分析始于1774年的一篇论文，分析过程本身却持续了40多年。有了拉普拉斯所打下的基础，我们将在下一章离开概率论的领域，而进入统计学的地盘。这两者的连捧点，就是所有数学和科学学科中最重要的曲线之一——钟形曲线，又被称为正态分布。这条曲线，以及随之而来的新的测量理论，将是下一章的主题。
 
第七章 测量与误差定律
 
数字似乎总是带有权威性。人们差不多都会——至少下意识地——认为：如果教师按100分制来打分，那即使是1分2分的微小差别，也一定真地意味着些什么。但如果连10个出版商都相信最早那部《哈利·波特》的手稿不值得出版的话，可怜的芬尼根太太（并非前面那位老师的真名）怎么可能如此精细地区分出两篇作文的好坏，来给一个打92分而另一个打93分呢？即使能够接受作文质量可以在一定程度上加以定义的观点，也仍应认识到分数并不是作文质量的描述，而更多地是对作文质量的测量。随机性对我们最重要的影响方式之一，就是影响测量。在这个作文的例子中，测量装置是教师，而教师给出的评价如同任何测量值一样，容易受随机变化和误差的影响。投票也同样是一种测量。此时所测量的，不是每位候选人在投票日当天得到多少人的支持，而是有多少人真正在乎这次选举并不嫌麻烦地跑去投票。
 
测量的不精确性是18世纪中叶的一个主要问题。在18世纪晚期出现的对测量之数学理论的需求，还另有一个原因：1780年代的法国兴起了一种新的严格的实验物理学方式。因此，一场对实验物理进行改革并使之数学化的运动发动了起来。其中，拉普拉斯再次扮演了主角。
 
拉普拉斯、拉瓦锡以及其他一些人——特别是进行电磁实验的法国物理学家查理-奥古斯丁·德·库仑（Charles-Augustinde Coulomb）——的成果，改变了实验物理学的面貌，此外在1790年代，还对一种新的有理单位制之发展作出了贡献。这个新单位系统——公制系统——的目的是要替代那些各自为政、阻碍科学发展并经常导致贸易纠纷的多个单位系统。
 
天文学和实验物理学方面的需求，意味着在18世纪晚期到19世纪早期，很大一部分数学家的任务，就是理解和量化随机误差。他们的努力带来了一个新领域：数学统计学。它提供了一整套工具来解释观测值和实验数据。统计学家有时认为，现代科学就是围绕着测量理论的建立而成长起来的。
 
因此，正确理解统计推理，不仅在科学工作中十分有用，在日常生活中也是如此。
 
2008年的一项研究中，志愿者们被要求给5瓶酒打分他们给标价为90美元的酒的分数，要高于另一瓶标价为10美元的酒，但实际上，狡猾的研究者们在两个瓶子里灌的是相同的酒。而且，实验中还对被试者的大脑进行了磁共振成像。结果表明，当被试者们品尝他们相信是更贵的酒时，被认为是对愉快体验进行编码的那个大脑区域，确实更为活跃。但在评判这些品酒行家之前，应该考虑到下面这一点：某研究者先问明30个喝可乐的人是否更喜欢可口可乐或百事可乐，然后再让他们品尝放在一起的两个牌子的可乐，以检验他们的偏好。30人中有21人都声称，品尝确认了他们的选择。实际上，不厚道的研究者将可口可乐倒进了百事可乐的瓶子，而将百事可乐倒进了可口可乐的瓶子。在进行评价或测量时，我们的大脑并非仅依赖于直接的感知输入，而是额外还结合了其他的信息源——比如期望。
 
这么多令人产生怀疑的原因，促使科学家们设计了多种方式，来直接测量品酒专家们对味道的分辨力。一种方法是酒味三角。每位专家被提供了3杯酒，其中两杯完全相同。他们的任务是找出那个不同的样品。1990年的一项研究中，专家能正确识别出不同样品品的几率仅为2/3，即大概每3次中有1次。还是这个实验中，一群专家被要求在包括酒精含量、是否含丹宁酸、甜度和果味度等12个方面给多种酒来打分。专家们的意见在9个方面上明显不一致。最后，在根据其他专家的描述来指出相应的酒的测试中，被试者的正确率仅仅只有70%。
 
但评分体系却仍然发展蓬勃。为什么呢？酒评家们发现，当他们试图用星级制或简单的好、坏或者糟透了这样的口语描述来概括酒的质量时，他们的意见并不令人信服；但如果用的是数字，那么购买者对于评价的态度就简直是崇拜了。数字分数尽管十分可疑，却能让购买者相信，他们从不同种类、不同酿酒商和不同年份葡萄酒的稻草堆中挑中的，就是那一枚金针
 
要使利用数字来下定论的质量测量方式确实能应用于一种酒——或一篇作文——之上，测量理论就必须解决两个关键问题：如何根据一系列不同的测量值来决定这个数？给定有限个测量值时，怎样才能估计出此数即为正确答案的概率？我们现在就来看看这两个问题，因为无论数据来源为客观或主观，问题的答案都是测量理论所要达到的目标。理解测量的关键，在于理解由于随机误差所造成的数据变化的本性。假设将若干种酒提供给15个酒评家，或在不同时间重复提供给某1个酒评家，或将两者结合进行，那通过得分的平均数或说均值，就可以干净利落地汇总酒评家对各种酒的意见。但重要的不仅仅是均值：如果所有15份酒评都认同某种酒的得分是90分，这传达了一种信息；而如果15个分数是80、81、82、87、89、89、90、90、90、91、91、94、97、99和100，这传达的又是另一种信息。两组数据均值相同，但数据与均值之间的差别却不同。由于数据点的分布方式如此重要，数学家们就创造了一个数值量度，来描述数据中的波动。这个数值被称为样本标准差。数学家有时还利用这个波动的平方来进行量度，它称为样本方差。
 
样本标准差描述了一簇数据与其均值之间的接近程度，或者用更实用的话来说，描述了数据中不确定性的大小。该值较小时，数据都落在均值附近。如所有酒评分都是90分的数据，其样本标准差为0，这告诉我们，所有数据都与均值相同。但当样本标准差较大时，数据就没有簇集在均值附近。那个取值在80到100的葡萄酒分数集，其样本标准差为6。根据一个经验规则可知，大多数评分与均值的差都落在6分之内。此时我们对这种酒所能真正给出的评价，是它的分数很可能落在84分到96分之间。
 
最早认为不同类型的测量数据也拥有共同特征的人之一，就是雅可布·伯努利的侄子丹尼尔。1777年，他将天文观测中的随机误差，与弓箭手所射箭支的飞行轨迹偏差做了类比。他推导说，在两种情况下，目标——被测量的真实值或靶心——都应该落在中心附近的某处，而观测结果则应聚集在它周围，而且，离目标较近的结果应该比远离目标的结果更多。他给出的描述这个分布的定律并不正确，但重要之处在于，他洞悉到弓箭手误差的分布，也能反映天文观测误差的分布。
 
误差分布服从某个普适定律——有时称为误差定律——是作为测量理论之基础的中心法则。它神奇地隐含着下面的推论，即当满足某些非常常见的条件时，通过同一个数学分析，就能根据测量值确定任意类型的真值。运用这样一条普适法则，根据天文学家的观测数据集来确定某天体真实位置的问题，就等价于在只知道箭支落点处小洞的位置时确定靶心位置，或根据一系列分数来确定葡萄酒“品质”的问题。这也是数学统计得以成为贯通一体的学科而非仅仅是一袋子小诀窍的原因。
 
这并不是说随机误差是影响检测结果的唯一一种误差。如果一群酒评家中的一半只喜欢红葡萄酒，另一半只喜欢白葡萄酒，而除此之外，他们都完全赞同彼此的看法
 
我们也将帕斯卡三角形某行的数字，以高度在条形图中表示出来的话，那么棣莫弗推导得到的近似就是一个很显然的结果。比如，在帕斯卡三角形第三行中的3个数字是1、2、1。在条形图中，第一个条形为1个单位高；第二个的高度是第一个的一倍；而第三个条形的高度又再次为1个单位。现在来看看第五行中的五个数字：1、4、6、4、1。这时的图中将有五根条形，且同样起始于矮条，在中间上升到顶点，然后又对称地降下来。那些非常下面的行，其系数会形成有非常多糸形的条形图，但行为方式却是一样的。帕斯卡三角形的第10行、第100行和第1000行所对应的条形图在139页中给出。
 
如果用一条曲线将这些条形的顶部连起来，就出现了一个特征形状——它们趋近于一口钟的形状。如果再将曲线弄光滑些，就可以写出它所对应的数学表达式。这条光滑的钟形曲线不仅仅是帕斯卡三角形里数字的图形化表示，更提供了一种既精确又好用的估计帕斯卡三角形中那些非常下面的行中系数的方法。这就是棣莫弗的发现。
 
今天，钟形曲线通常被称为正态分布，有时也叫高斯分布（我们将在后面看到这个名称的由来）。正态分布实际上并不是一条固定的曲线，而是一族曲线，其位置与形状由两个参数来确定。第一个参数确定了曲线峰值出现的位置，在此图中，峰的位置分别为5、50和500；第二个参数则确定了曲线的散布程度。这个散布程度的现代名称——标准差——直到1894年才出现，同时也正是早先所说的样本标准差这个概念的理论对应物。粗略来说，标准差等于曲线上值约为最大值的60%之两点间宽度的一半。如今，正态分布的重要性已远远超出了近似帕斯卡三角形中数字的用途。实际上，它是我们所发现的最普遍的数据分布方式。
 
当用于描述数据分布时，钟形曲线表明，进行多次观测后，大多数结果将落在均值附近。曲线的峰就表明了这一点。不仅如此，当曲线对称地朝两边逐渐降低时，它给出的，是得到特定观测结果——大于均值与小于均值的结果——的次数是如何逐渐减小的。在服从正态分布的数据中，大约68%（差不多2/3）的观测值将落在距均值为1倍标准差的范围之内，大约95%落在2倍标准差的范围内，而99.7%的观测值都落在了3倍标准差的范围内。
 
对于许多调查而言，大于5%的误差幅度都不可接受。但在日常生活中，我们却常常根据远少于必需的数据量来进行判断。因此，在评价他人在以上方面所取得的成功时，我们的判断仅仅只依赖于少数几个数据点。
 
当看到一次成功或失败时，我们所观察到的只是一个数据点，一个钟形曲线上的采样，它仅仅代表了那早已存在的可能性之一。我们无法得知这个单独的观测所代表的，到底是均值本身，还是某个“例外值”；也无法知道这个观测所对应的，到底是我们有把握赌一把的事情，还是某个不大可能再次产生的罕见情况。但至少应当清楚，一个采样点就是一个采样点，相比于简单地将其作为真实情况来接受，我们更应在产生该采样点的标准差或概率分布这个语境下来认识它。这瓶葡萄酒的分数可能是91分，但如果没有足够信息来估计这同一种酒被多次评分或交由其他人评分的过程中可能发生的分数变动的话，91分这个数字就毫无意义。
 
认识到正态分布描述了测量误差的分布，则是棣莫弗取得成果之后数十年的事了。发现这一点的人是德国数学家卡尔·弗里德里希·高斯（Carl Friedrich Gauss），他的名字也常常与钟形曲线联系在一起。高斯在解决行星运动问题时开始认识到正态分布的这个性质
 
将正态分布从角落中拉出来的人是拉普拉斯。他于1810年接触到高斯的著作，而之前不久，他才刚刚在法兰西科学院宣读了一份备忘，证明了一条称为中心极限的定理，该定理称，大数量独立随机因素总和之取值为任意给定值的概率，服从正态分布。比如，假设你烤100条面包，每次都按生产1000克面包的配方来进行。由于随机性，你可能会有时多加一点或少加一点面粉或牛奶，或者在烘烤时多烤掉一点或少烤掉一点水分。最终，这许许多多的因素会使你的面包多个几克或少个几克，但中心极限定理告诉我们，这些面包重量将服从正态分布。
 
今天，中心极限定理和大数定律成为了随机性理论中最为著名的两个结果。
 
为了说明中心极限定理如何解释正态分布确实是正确的误差定律，让我们再来看看丹尼尔·伯努利的弓箭手例子。每个随机因素——比如瞄准的误差、气流的影响等——都会使我射出的箭在垂直方向上偏离目标，或者高些或者低些，两者出现的可能性相等。
 
所有这些误差都会使箭朝同一个方向偏离，从而使箭或高或低地远离目标。问题是：这些误差正好相互抵消，或正好累加形成最大误差，或取值在前两者间任意一点处，各自的可能性有多大？这些影响因素形成了一个伯努利过程——就如同扔硬币并问扔出某个特定次数的正面的可能性有多大一样。帕斯卡三角形描述了问题的答案，或者当试验次数很多时，正态分布给出了答案。这也正是中心极限定理所说的内容。
 
到1830年代，大多数科学家已经开始相信，每个测量值都是一个复合物，受到很多误差源的影响，并因此服从误差定律。由此，误差定律和中心极限定理便使我们能获得对数据及其与物理现实之间关系的崭新且更为深刻的理解。
 
第八章 混沌中的秩序
 
我们总将随机性与无序联系在一起。
 
当19世纪的科学家们钻研新近才能获得的社会学数据时，不论何处，生命的混沌似乎总形成可量化可预测的模式。但使人震惊的不仅仅是这些规律性，更包括数据变动的特性。他们发现，社会学数据也常常服从正态分布。
 
如果像配第所相信的那样，人口的数量及增长反映了政府的优劣，那么，缺少测量人口数量的好方法，就会使评价政府质量变得十分困难。格朗特在此问题上展开了他最为著名的计算，特别是对伦敦人口的计算。从死亡表中，格朗特知道了出生人口的数量。而有了出生率的粗略估计，就可以推算出育龄女性的大概数量，进而估计家庭数量，再通过他自己观察到的伦敦城家庭成员的平均数量，就能估计出全城人口。他的计算结果是384000——而之前人们都觉得是200万。格朗特还证明，该城人口增长的主要贡献，来自于边远地区的移民，而非更为缓慢的人口繁衍；此外，尽管仍有瘟疫造成的恐惧，但即使是最严重的疫病所造成的人口减少，也总是在两年之内就得到了恢复。这一结论颇为令人吃惊。此外，格朗特还被认为发布了第一份“寿命表”，时至今日，这个系统化的预期寿命数据排列方式，仍被对人们寿命感兴趣的组织——从人寿保险公司到世界卫生组织——所使用。
 
格朗特的遗产在于，他表明通过仔细分析数据的有限样本，可以得到有关人群总体的推论。尽管格朗特与其他人进行了卓绝的努力，以便能利用简单的逻辑来了解数据中的信息，但要解释这些数据中的大部分秘密，还有待于高斯、拉普拉斯和其他19世纪及20世纪早期的科学彖们所发展起来的工具——“统计”
 
正态分布描述了许多现象围绕某中心值发生改变的行为方式，这个中心值就代表了现象的最可能输出值。在其《概率的哲学导论》（Essai philosophique sur les probabilites）一书中，拉普拉斯称这门新的数学学科能用于评判法庭证言、预测结婚率、计算保险费等，因此，继承与发展其构想的任务，就落到了一名年轻人——1796年2月22日出生于佛兰德的根特（Ghent，Flanders）的阿多夫·奎特雷（Adolphe Quetelet）——身上。
 
奎特雷回到布鲁塞尔后，就开始收集和分析人口统计数据，并很快将注意力集中在法国政府于1827年开始发布的犯罪活动记录上。在《论人及其能力的发展》（Sur I' homme et le developpement de ses facultes）这部发表于1835年的两卷本著作中，奎特雷印上了一张1826年至1831年所报道的法国各年谋杀案数量的表。他注意到，谋杀案的数量相对恒定，而且，每年用火枪、剑、小刀、木棒、石头、砍刺器具、拳脚、绳勒、溺毙和火烧等方式进行的谋杀案，其比例也相对恒定。奎特雷还按年龄、地域、季节、职业以及是否身处医院和监狱，来对死亡率进行分析。他还对酗酒、精神病和犯罪进行了统计学研究。此外，他在巴黎自缢者人数以及比利时60多岁老妇配20多岁小伙子的婚姻数量上，也发现了描述它们的统计规律性。
 
统计学家们之前就进行过类似研究，但奎特雷比他们做得更多些：他不仅观察数据的平均值，还仔细研究了它们偏离平均值的方式。不管研究对象为何物，奎特雷都遇到了正态分布：
 
奎特雷无意中得到了一个有用的发现：随机性的模式是如此值得信赖，以至于在某些社会学数据中，对该模式的违背，可作为指证坏事的证据。如今，这种分析被应用于奎特雷的时代所不可能处理的大量数据上。实际上，在近几年中，类似的统计侦察术正逐渐流行，并创造了一个称为法律经济学的新领域，作为其最著名案例的统计研究，
 
奎特雷认识到，通过将人们置于大量的实验环境中，并测量其行为，可以对一门真正科学中的理论加以检视。由于这个方法实际不可行，所以他相信社会科学更类似天文学而非物理学，其理论的洞察需要通过被动的观测来获得。
 
对于有限数据集而言，它总无法与正态分布曲线完美匹配。在早期的统计学中，科学家们简单地将数据作图，然后观察所得曲线的形状，来判断这些数据是否按正态分布。但应该如何量化这个曲线匹配的精确程度呢？皮尔森发明了一种称为χ2检验的方法，可以确定一个数据集是否确实服从我们所认为的分布。1892年，他在蒙特卡罗演示了这个检验方法。他所进行的测试可以看作是贾格之事迹的严格复制品。如贾格所碰到的情形一样，在皮尔森的测试中，轮盘赌开出的数字并不服从所期望的分布，即当轮子确实产生随机数时所应服从的分布。另一次测试中，皮尔森观察了在将12枚骰子扔出26306次时，每次中扔出的5点和6点的骰子的数量。他发现这个分布同样不满足使用完美骰子进行公平赌赛时所应得到的分布——在公平的情况下，一枚骰子扔出5点或6点的概率是1/3，或说0.3333；实际的分布却与此概率为0.3377时的分布相一致——换句话说，骰子是歪的。

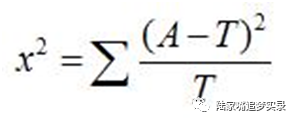
今天，χ2检验得到了广泛运用。假设现在不是对骰子、而是对3盒麦片进行检验，以观察消费者对它们的喜好程度。如果消费者们没有特殊的偏好，那么可以期望，每盒麦片都会被近1/3的消费者所选购。如我们已经看到的，真实结果很难如此均匀地分布。使用χ2检验就能确定，得票最多的那盒麦片，它的胜出的确是由于消费者的偏爱而非碰巧的可能性有多大。类似地χ2检验能帮助这位CFO来迅速判断，到底是假设正确，还是说新店是个偏离典型的例外，而公司此时最好将各种车型的比例进行相应调整。
 
爱因斯坦1905年的统计物理学论文，其目的是要解释一种被称为布朗运动（Brownianmotion）的现象。该过程以罗伯特·布朗（Robert Brown）的名字命名。此人是植物学家，使用显微镜的世界级专家，而且被认为是第一个对细胞核作出清晰描述的人。

透过目镜，布朗注意到，他所观察的花粉迸裂所释放出的微粒似乎在运动。尽管花粉是一种生命之源，其本身却不是有生命的物体。但不管布朗盯上多久，运动却从不曾停止，就好像这些微粒拥有某种神秘的能量似的。这个运动似乎没有特定的目的地；实际上，它看起来完全随机。无比激动的布朗首先得出的结论，是他已经找到了所追寻的东西，因为这种神秘的能量，除了是为生命提供动力的能量之外，还能是什么呢？
 
接下来的一个月里，布朗勤勉地进行了一系列实验，并发现，对于所有他能搞到手的各色有机小颗粒——诸如分解了的小牛肉纤维、“被伦敦的灰尘染黑的”蜘蛛网、甚至他自己的黏液等，当它们悬浮于水中或——有时——于杜松子酒中时，都能观察到同样的运动。然后，他期盼的解释遭到致命一击：当他用石棉、铜、铋、锑和锰之类的无机小颗粒进行实验时，观察到了同样的运动。此时他认识到，所观察到的运动根本与生命无关。事后将证明，布朗运动的真实原因，与产生奎特雷所注意到的人类行为规律性的力量一样，不是一个实在的物理力，而是产生于随机模式的虚拟力。
 
理解布朗运动的基础，是玻尔兹曼、麦克斯韦与其他人在布朗的发现之后数十年间打下的。受奎特雷的启发，他们建立了统计物理学这一新领域，运用概率与统计的数学思想，来解释构成流体的（当时仍然是假想的）原子之运动是如何造就流体性质的。爱因斯坦使用这个新生的理论，通过详尽的数学描述，解释了布朗运动的准确机制。统计学方法对于物理学的必要性，从此不再存有疑问，而物质由原子和分子组成的观点，将成为大多数现代技术的基础，同时也是物理学史上最为重要的思想之一。
 
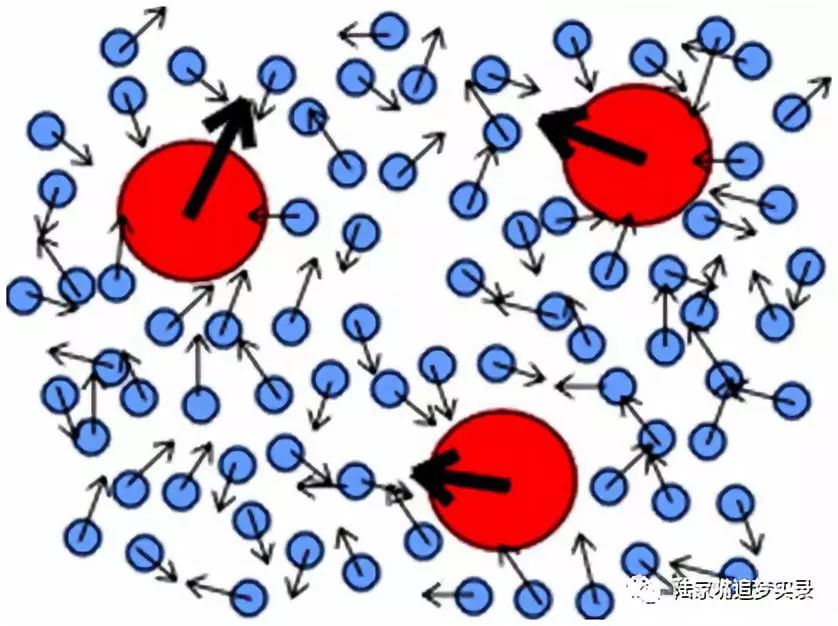
在路径上的某些点上，运动方向发生随机改变——常常被称为醉汉的脚步。
 
按原子论的预言，如果漂浮于液体中的颗粒一直不断地被液体分子随机地轰击，那么可以预计，颗粒将因为这些碰撞，一会儿朝这边一会儿朝那边地动来动去。但布朗运动的这幅图景中存在两个问题：首先，对于可见的悬浮颗粒而言，分子实在是太小了，无法推动颗粒移动；其次，分子的碰撞发生得远比所观察到的颗粒晃动要来得频繁。爱因斯坦天才想法中的一点，就是认识到这两者其实会相互抵消：尽管碰撞发生得非常频繁，但由于分子如此之轻，所以这些频繁而独立的碰撞不能产生可察觉的效果。只有在某些时候，纯粹的运气使得某个方向上的撞击具有了优势——才会发生足以使人注意的晃动。爱因斯坦在计算中发现，尽管有着分子层面上的混沌，但在分子的参数如大小、数量和速度等，以及可观察的颗粒晃动频率与幅度之间，存在着可预测的关系。有史以来头一遭，新的可观测的结果与统计物理学，被爱因斯坦联系在了一起。
 
这是一个伟大原则的胜利：许多我们感知的自然界秩序，在其掩饰之下，都是看不见的无序，而这些秩序也只有通过随机性的法则才能理解。正如爱因斯坦所言：“能认识到那些看来与直接而可见的真理颇有出入的现象，其实可以被统一为一体，这种感觉无比美好。”
 
在爱因斯坦的数学分析中，正态分布再次扮演了核心角色，并达到了科学史上一个新的辉煌地位。醉汉的脚步也就此确立了最具基础性、并很快得到最多研究的自然过程之一的地位。
 
尽管在随机变化中，存在着有规律的模式，模式却并非总是有意义的。当模式中存在意义时，我们应该去发现它；但同样重要的，则是当模式实际并无意义时，就不该试图去抽取出“意义”。要避免随机模式“有意义”的错觉，是一件困难的工作。
 
第九章 模式的错觉与错觉的模式
 
1850年代初，被称为“敲桌子”的这种灵魂接触方法，以及技出同门的“移桌子”和“翻桌子”，在欧美风靡一时。这些通灵法由一群人参与，他们围坐在桌旁，手放在桌上，然后就是等待。在“敲桌子”中，一段时间的等待后，就会听到一声敲打声；而在“移桌子”和“翻桌子”中，桌子则会开始翅起或移动，有时甚至拽着坐在桌旁的人一起移动。有人还画下了那些严肃的、穿着长到大腿中部的夹克的大胡子男人们，以及穿着带裙撑长裙的热衷的妇女们，当他们的手跟随桌子移来移去时，眼睛因惊奇而瞪得老大。“移桌子”变得如此流行，使得科学家们在1853年夏天时开始对之进行研究。一组医生注意到，在那段静坐的时间里，一种无意识的共识似乎逐渐成形，以决定桌子移动的方向[2]。他们发现，如果分散在座者的注意力以阻止共同期望形成的话，桌子就不会动。在另一项实验中，他们成功构造出一种情况，使半数参与者希望桌子往左移，而另一半参与者则希望它往右移，从而也使得桌子不发生移动。
 
给这个问题画上句号的研究，是由物理学家迈克尔·法拉第（Michael Faraday）——电磁理论的创始人之一，电机的发明者，历史上最伟大的实验科学家之一——所完成的。和那些医生们一样，法拉第的结论是，这些坐着的参与者们无意识地拉动或推动着桌子。运动也许是由于不耐烦而随机发生的，然后在某个时刻，这些参与者们在随机运动中感知到了某个模式，而当被试者们的手跟随这个想象中的桌子移动的带领时，该模式便成为了某种自我实现的期望。法拉第认识到，人类感知并不是实在的直接结果，而是想象活动的结果。
 
感知需要想象，因为生活中所遇到的数据从来都是不完整且模棱两可的。举例来说，多数人都认为，没有什么证据比亲眼所见更加可靠，而在法庭上，也没有什么比目击证言更受尊重的了。但如果在法庭上展示一段成像质量与人类视网膜上形成的未经处理的数据完全一样的视频，那法官可能就会想，你到底在拖延些什么。首先，这段影像中会有一个盲点，即视觉神经与视网膜的连接点。其次，在视野中，唯一具有足够高分辨率的区域，不过是围绕视网膜中心大约1度视角的范围，这个范围大致相当于将手臂伸直时大拇指所对应的宽度。在这个区域之外，分辨率急剧下降。作为补偿，我们不停地移动眼球，以便成像分辨率高的区域能落在希望看到的场景的不同部分上。因此，送往大脑的原始数据，是一幅晃来晃去、酩酊大醉的图像，里面还有一个洞。幸运的是，大脑会对这些数据进行处理，将双眼传来的输入加以组合，并在相邻位置上的视觉特征相似且可内插值的假设下，来填充图像中的空隙[7]。最后的结果——至少在年老、受伤、疾病或过量的麦泰酒造成严重损伤之前——就是一个快快活活却承受着他／她的视觉既敏锐又清晰之错觉的人类。
 
我们还利用想象取巧地填补非视觉数据模式中的空当。如同视觉输入一样，我们根据不确定和不完整的信息，来作出结论并进行判断；而完成模式分析后的结论是，我们所得的“画面”清晰又准确。但真是如此吗？
 
在防止辨识出虚假模式的方向上，科学家们已经开始了迈进。通过发展统计分析方法，能判断一组观测值是否能对某个假设提供足够好的支持，或相反地，它们那表面上对假设的支持，是否完全是偶然性所致。
 
这类技巧之一的显著性检验，是由20世纪最伟大统计学家之一的费希尔（R．A．Fisher）于1920年代发展起来的。
 
为了说明费希尔的思路，设想在一项超感官知觉研究中，参与的学生要预测扔硬币的结果。如果观察发现她差不多每次都能正确预测出结果，我们就可能形成假设，即她确实具有这方面的能力，比如通过意念力来预测。另一方面，如果她能正确预测出差不多半数的结果，那么这个数据支持的假设就是她只不过在瞎猜而已。但如果结果落在两者之间，或者根本就没有足够多的数据时，又该如何呢？在接受与拒绝这两个对立的假设之间，决策的分界线应该画在哪儿呢？这就是显著性检验所做的事情：它是一个规范的计算方法，用来计算如果所检验的假设为真时，我们能观测到所得数据的概率。如果这个概率小，我们就拒绝假设；反之则接受假设。
 
显著性检验与其他统计方法对科学家提供了很好的帮助，特别是在大规模的受控研究中。不过，我们平常并不会进行这样的研究，也不会下意识就能用统计分析来加以处理。我们依靠的是本能。如果我的维京牌炉灶存在缺陷，而凑巧一个熟人也告诉了我同样的事情，那我就会告诫朋友们不要买这个牌子的炉子；如果在好几次乘坐联合航空（United Airlines）班机时，同机的乘客似乎总比最近坐过的其他航空公司航班的乘客更为乖戾的话，我就会避免继续乘坐联航的班机。这些情况中，数据量并不大，但我们内在的本能却找到了模式。
 
这些模式有时有意义，有时没有。不论是哪种情况，我们对生活中各种模式的感知既高度可信却也高度主观。这一事实有着深远的含义。它隐含了某种相对性。现代社会中的许多假设，都像“移桌子”一样，建立在共享的错觉之上。
 
寻找模式并赋予其意义是人类的天性。卡尼曼和特沃斯基分析了在评价数据模式及面临不确定性进行决策时所使用的许多简化方法。他们称这些简化方法为“启发式方法”。一般情况下，启发式方法十分有用，但正如我们处理视觉信息的方式有时会带来视觉错觉一样，启发式方法有时也会导致系统性错误。卡尼曼和特沃斯基称这种错误为“偏误”。我们都使用启发式方法，同时也都受到偏误的影响。不过，尽管视觉错觉很少与日常体验发生关系，认知偏误却在决策中扮演着重要的角色。
 
“人们对于随机性只有很糟糕的概念：他们对随机性视而不见，而当他们试图去产生随机性时，也无法做到”，更糟的是，我们总是照例地误判了机遇在生活中的角色，并总是做出与我们的最大利益确不相符的决定。
 
设想有一个事件序列。这些事件可以是季度赢利，或是通过因特网约会服务获得的一串或好或糟的约会。不管是哪种情况，序列越长，或者对更多的这种序列进行观察，就越有可能发现所有那些想象得到的模式——而这些“模式”完全是凑巧的结果，根本就不需要有个什么“原因”来造成那一连串或好或糟的季度、或好或糟的约会。数学家斯潘塞-布朗（George Spencer-Brown）充分展示了这一点。他指出，在101000007个0或1构成的随机序列中，我们应当预计到，至少会出现10个互不重叠的、由100万个连续的0所构成的子序列。
 
斯潘塞-布朗的要点在于，一个过程本身是随机的，并不同于这个过程产生的结果看起来是随机的。
 
对于随机模式感知进行的最早期的思索之一，出自哲学家汉斯·赖欣巴哈（Hans Reichenbach）。他在1934年写道，未受过概率论训练的人们难以识别出随机事件序列。看看下面这个扔200次硬币所得到的结果序列，其中Ⅹ表示反面朝上，而〇表示正面朝上：〇〇〇〇ⅩⅩⅩⅩ〇〇〇ⅩⅩⅩ〇〇〇〇ⅩⅩ〇〇Ⅹ〇〇〇ⅩⅩⅩ〇〇ⅩⅩ〇〇〇ⅩⅩⅩⅩ〇〇〇Ⅹ〇〇Ⅹ〇Ⅹ〇〇〇〇〇Ⅹ〇〇Ⅹ〇〇〇〇〇ⅩⅩ〇〇ⅩⅩⅩ〇ⅩⅩ〇Ⅹ〇ⅩⅩⅩⅩ〇〇〇ⅩⅩ〇〇ⅩⅩ〇Ⅹ〇〇ⅩⅩⅩ〇〇Ⅹ〇〇Ⅹ〇Ⅹ〇ⅩⅩ〇Ⅹ〇〇〇Ⅹ〇Ⅹ〇〇〇〇ⅩⅩⅩⅩ〇〇〇ⅩⅩ〇〇Ⅹ〇ⅩⅩ〇〇〇Ⅹ〇〇〇ⅩⅩ〇Ⅹ〇〇ⅩⅩ〇〇〇〇Ⅹ〇〇ⅩⅩⅩⅩ〇〇〇〇ⅩⅩⅩ〇〇〇Ⅹ〇〇〇ⅩⅩⅩⅩⅩⅩ〇〇ⅩⅩⅩ〇〇Ⅹ〇〇Ⅹ〇〇〇〇〇ⅩⅩⅩⅩ。我们可以很容易地找到数据中的模式——比如，开始时跟在4个Ⅹ后面的4个〇，以及快结束时出现的连续6个Ⅹ。数学计算表明，这类模式很可能会出现在200次扔硬币的结果序列中，但仍有许多人对之感到吃惊。如果这些Ⅹ和〇的字符串代表的不是扔硬币的结果，而是对我们产生影响的事情，那么人们就会为它们寻找有意义的解释。如果一串Ⅹ代表股市连续下跌的日子，人们就会相信那些宣称股市即将崩溃的专家观点；如果一串〇代表你最爱的运动明星连续获得的好成绩，那么那些大夸该运动员“稳定表现”的话语，听起来就十分令人信服
 
学术界及作家们已经投入了大量精力，来研究金融市场中的随机成功事例的模式。比如，许多证据表明，股票的表现是随机的——人们根本就无法从随机变动中获取任何利益。仅仅靠偶然因素，某些分析师或基金也总能表现出令人印象深刻的成功模式。许多研究都表明，这些市场中以往的成功事例，并非是未来成功的一个良好指标——即这些成功很大程度上不过是走运而已。尽管如此，大多数人还是觉得，他们的股票经纪人或运营基金专家们所提供的建议是值得花钱的。
 
1995年的一项研究显示，Barron's杂志每年都会邀请8~12名薪金最高的“华尔街超级明星”，举行圆桌会议来推荐股票。但这些股票的收益，也仅仅只是和市场的均回报率相当。当然，如斯潘塞-布朗的例子所示，如果我们观察足够长的时间，就肯定会碰到某个家伙，他仅仅靠运也能做出令人称奇的成功预测。
 
米勒是美盛价值信托基金（Legg Mason Value Trust Fund）的唯一经理，而在其15个连续成功的年头中，基金表现每年都好于标准普尔500指数。由于这个成就，米勒被《金钱》（Money）杂志誉为“1990年代最伟大的资金经理”，在米勒连胜的第14年时，CNNMoney网站曾引用某分析师的话，称纯靠运气而获得连续14年成功的机会是1/372529
 
学术界把这种将随机重复归因于超优异表现的错误认识称为“热手谬误”。热手谬误的大多数研究工作开展于体育运动领域，因为在体育运动中可以很容易地定义和衡量表现；同时，体育比赛的规则清晰而确定，数据充分而公开，感兴趣的情况也能一再复现
 
对热手谬误的兴趣产生于1985年前后，更具体点，它出现在特沃斯基与同事的一篇《认知心理学》（Cognitive Psychology）期刊论文中。在名为《篮球运动中的热手：论对随机序列的错误感知》的文章中，特沃斯基和同事们研究了大量的篮球比赛统计数据。当然，球员天赋各不相同：有的投篮命中率为50%，有的更多些，有的更少些；每名球员也都有过一段时间中手热或手冷的经历。文章作者的问题是，假设每一次投篮的中与不中是随机决定的话，此时应观察到的手热期或手冷期的次数及长度，与实际的次数及长度相比是怎样的？也就是说，如果球员们并不是在投篮，而是在扔一枚能够反辨其命中率的不完美硬币时，所得的结果是怎样的？研究者们发现，尽管存在着连续命中或连续投失的情况，费城76人（Philadelphia 76ers）的投篮，波士顿凯尔特人（Boston Celtics）的罚篮，以及受控实验中康奈尔大学（Cornell University）男子和女子篮球队的投篮，都未显示出任何存在非随机行为的证据。
 
对运动员表现“稳定性”的一个具体而直接的衡量标准，就是在上一次投篮成功（即投中一球）的前提下，本次投篮也成功的条件概率。对于发挥稳定的球员，这个条件概率应该比他／她的总成功率要高。但论文作者们发现，对于每名球员，紧跟在一次成功之后的成功，与紧跟在一次失败（即投篮不中）之后的成功，两者的可能性相等。
 
特沃斯基的论文发表几年后，诺贝尔奖得主、物理学家普塞尔决定也来研究一下棒球运动中稳定表现的本质，他的发现——用他的哈佛同事古尔德的话来说——就是除了迪马吉奥连续56场都能击中球这个例外，“在棒球运动中，从没发生过什么比扔硬币模型预测所得频率更常发生的事情”。
 
相比于好的球员和球队，糟糕的球员和球队会出现持续更久的连续失败，而且出现连败的频率也更高些；而相比于差一些的对手，好的球员和球队会出现更长的连胜，同时出现连胜的频率也更高些。但这是由于他们平均的败率或胜率要高一些。该平均比率越高，随机产生的连败或连胜就越长且越频繁。我们只需要理解扔硬币是怎么回事，就可以理解上面的情况了。
 
那么米勒的连续成功又是怎么回事呢？如果知道其他几个统计数字，就不会那样震惊于米勒的稳定表现是某个随机过程产物这一事实了。比如，在2004年，米勒的基金赢利不过是12%不到一点，而标准普尔中的股票平均赢利为15%多。这么听起来，这一年标准普尔应该击败了米勒，但实际上，2004年被归入了米勒“获胜”的一栏，因为标准普尔500指数不是股票价格的简单平均，而是按各公司资本额对其股票加权后的均值。米勒的基金比标准普尔股票的简单平均要差，但却比加权平均要好。事实上，在其连续成功那些年的30来个“12个月时间段”中，他做得还不如加权平均好，但这些时间段都并非正好是整日历年，而他的连续成功是按1月1日到12月31日的日历年来计算的。因此从某种意义上来说，他的连续成功从一开始就有些虚假的味道，因为这个成功的定义方式正好对他奏效了。
 
在讨论米勒2003年的表现时，为《融会贯通的观察家》（The Consilient Observer）时事通讯[由瑞士信贷第一波士顿公司（CreditSuisse-First Boston）出版]撰稿的作家们称，“在过去40年中，没有其他任何一支基金的表现，能连续12年优于市场”。他们提出了一个问题：纯靠运气做到这一点的概率是多少？接着，他们给出了3个估计值（这一年是2003年，而他们考虑的，是一支基金在区区12个年头中连续击败市场的概率）：1/4096，1/477000，以及22亿分之1。借用爱因斯坦的话说，如果他们估计正确，那么只需要一个值就够了。真正的概率是多少呢？大致等于3/4，或说75%。这个差别实在有些悬殊，因此我最好来解释一下。得出那些极低概率值的人，在某个意义下是对的：如果你正好在1991年开始时正好挑出了米勒这么个人，而完全出于偶然，这个你挑选的人不多也不少地在下面15年中击败了市场，那这个可能性的分母就的确是个天文数字。这一概率也是在15年中每年扔一次硬币并次次都扔出正面的概率。但正如对马立斯的本垒打分析中那样，这并不是真正与问题有关的概率，因为除了米勒之外，还有着数以千计的基金经理（目前有6000多名），同时，还有许多个15年的时间段可以用来完成这一丰功伟业。因此，真正相关的问题是，如果几千人每年都扔一次硬币，并且一直这样做了好几十年，那么其中的某一人，在某个15年时间段中，能够全部扔出正面的机会是多大？这个值就远大于简单地连续扔出15次正面的机会。
 
为了使解释更具体些，假设有1000名基金经理——这肯定是个低估的数字——从1991年（米勒的连胜开始的那一年）开始，每年都扔一次硬币。第一年，这些人中的大约一半会扔出正面；过两年后，大概有1/4的人会扔出两次正面；过3年后，大概有1/8的人扔出3次正面；依此类推。那些扔出反面的人逐渐退出了游戏。这并不会影响我们的分析，因为他们已经失败了。在15年后，某个特定的扔硬币者一直扔出正面的概率为1/32768。但是，从1991年开始扔硬币的这1000人中的某一个能一直扔出正面的机会则大得多，大约为3%。最后，我们没有理由只考虑那些从1991年开始扔硬币的人——这些经理们可以从1990年或1970年或现代基金时代中的任意一年开始扔硬币。既然《融会贯通的观察家》的作者们用的是40年这个值，我就来算一算，在过去40年中，某个经理能在某个15年时间段内，每年都击败市场的概率。如此一来，机会就增加到了之前所给的值，即差不多3/4。
 
至此我引用了一些体育和金融领域中热手谬误的例子。但是，在生活中的方方面面，都能碰到连续的成功或失败，或其他特定的成功与失败模式。有时成功是主流，有时则是失败。不管是哪种方式，生活中重要的是将眼光放长远，并能理解不管是连续的成功或失败还是其他看似不像随机序列的模式，都确实可能是纯运气的结果。同样重要的是，当评价他人时，我们应该认识到，在一大群人中，如果没有人经历过长时期的连续成功或失败，这才真是很奇怪的一件事。
 
尽管我所作的这类分析似乎被那些为媒体所引用的许多观察家们所遗忘，但对于从学术角度来研究华尔街的人来说，却根本不是什么新闻。比如，诺贝尔奖获得者、经济学家默顿·米勒（Merton Miller）说每个人都必须根据所处的环境来得出自己的结论，但了解了随机性的运作方式，这个结论至少不会太天真。
 
前面讨论了我们是怎样被那些在一段时间中产生的随机序列里的模式所愚弄的。但空间的随机模式同样具有误导性。
 
要揭示数据的含义，最清晰的方式之一，就是通过某种图像或图形来显示它们。当观察以此种方式呈现的数据时，那些很可能被忽略的有意义的关系会变得更明显。但这个做法的代价是，有时我们也会感知到一些实际没有意义的模式。我们的大脑就是被创造得如此行事的——吸收数据，填充空隙，然后寻找模式。举例而言，看看下面这幅图中灰色方块的排列。这张图看上去并不像一个名副其实的人，但我们可以从这个模式中得到足够的信息，
 
二战即将结束时德军的 V2火箭开始倾泻到伦敦城里。这些火箭非常可怕，其飞行速度是音速的5倍，很快，报纸就公开了火箭落点分布图，其中似乎可以看到并非随机而是有目的性的成簇的落点。对于某些观察家而言，这一簇簇落点体现了火箭飞行轨迹的控制精度。由于火箭飞行距离很长，因此，这些模式似乎表明，德国人的科技水平已经达到了一个大家做梦都想不到的先进程度。1946年，上述轰炸数据的数学分析结果发表于《精算学会杂志》（Jourruz I of the Institute of Actuaries）。作者克拉克（R．D．Clarke）将所研究的区域分为边长0.5千米的576个正方形小格子。这些格子中的229个从未遭到轰击，而另一方面，尽管格子的面积很小，却有8个格子遭到了4到5次轰击。不过，克拉克的分析表明，跟前面那个扔硬币的数据一样，这些数据的总体分布模式符合随机分布。
 
我们至此考察了若干随机模式愚弄人们的方式。但心理学家并不满足于仅仅对这些误解进行研究与分类，他们还研究了人们之所以会受到愚弄的原因。现在，我们把注意力转向这些原因中的某一些。
 
人们喜欢对周围的环境施加控制。有些人灌了半瓶苏格兰威士忌后还照样开车，却在飞机遇上一点小小颠簸时就吓得举止失常，原因就在于此。这种控制欲并非毫无缘由，因为自我控制的感觉，已经与自我感知和自尊融为一体。实际上，我们能做的对自己最有好处的事情，就是找到种种方式来控制自己的生活——或至少找到方式来让我们觉得的确控制了自己的生活。
 
人类对控制权的需要，与讨论随机模式有何关系呢？因为如果事情是随机的，那我们就没有做主；而如果我们做主的话，事情就不会是随机的。因此，在自觉掌握控制权的需要与认识随机性的能力之间，存在着根本的冲突，同时也是错误解释随机事件的主要原因之一。实际上，诱使人们将幸运误认为是能力，或将无目的的行动误认为是在进行控制，这是心理学研究者最容易做到的事情之一。
 
人们可能口头上会认同偶然性的概念，但他们却按偶然事件能被控制一样来行事。”随机性在真实生活中的角色，远不像在朗格的实验中那样明显，而我们对结果以及控制结果的能力则更为投入。因此，在真实生活中抗拒这种控制的错觉就越显困难。
 
在经历了一段时期的成功或失败的组织机构中，常能见到这种错觉的一个表现：成功或失败很容易被归因于头头的身上，而不是归因于运气以及造成机构目前总体状况的无数环境因素。在体育运动中，这一点尤为明显。如果在随机型任务的结果最终揭晓之前，还进行了一段时间的战略安排（那开不到头的会议），或当任务需要主动参与时（那些呆在办公室里的漫长时间），或当竞争存在时（从来就没有竞争这回事，不是么？），对于偶然事件的可控错觉，在金融、体育以及——特别是——商业环境中进一步强化。与可控错觉做斗争的第一步，就是要认识到它的存在。但即使做到了这一点，前路仍然艰苦，一旦我们认为我们发现了一个模式，这个念头就不会被轻易放弃。
 
一旦被错觉所掌控——如哲学家弗朗西斯·培根（Francis Bacon）于1620年所写的：“人类的理解力一旦采纳了某个想法，就会收集任何能证实该想法的例子，哪怕反例可能数量更多而且更有分量，但人类的理解力要么不去注意它们，要么就干脆拒绝接受它们，以此保证所采纳的观点仍能维持那不可动摇的地位。”
 
更糟的是，我们不仅有偏向性地寻找证实预设观念的证据，而且还会对有歧义的证据进行偏向于我们想法的解释。这是个大问题，因为数据常常都具有歧义。因此，通过忽略某些模式并强调其他一些模式，聪明的大脑可以强化它的信念，即使在缺乏确有说服力的数据时也是如此
 
确认偏误在现实世界中造成了许多不幸的后果。如果一名教师开始时相信某个学生比另一个要聪明，那他就会有选择性地将注意力集中在倾向于证实这一猜想的证据上。如果一名雇主对一个符合其预想的应聘者进行面试，那他通常会迅速形成第一印象，然后将剩下的面试时间用来寻找支持这个印象的信息。如果临床咨询顾问被提前告知某受访者生性好斗，那么他们将倾向于得出受访者确实好斗的结论，哪怕该受访者实际并不比普通人更加好斗。如果
 
人类的大脑已进化到能高效进行模式识别的水平。但正如确认偏误所显示的，我们集中于发现和确认这些模式，而不是将错误结论降到最少。但无需感到悲观，因为克服偏见仍然是可能的。仅仅认识到偶然事件也能产生模式，是一个开始；如果能学会对我们的观点和理论提出疑问，则又是一大步。最后，我们应该学会用同样多的时间，不但去寻找我们之所以正确的原因，更要去寻找证明我们错误的证据。
 
第十章 醉汉的脚步
 
1814年，差不多在牛顿物理学成功的巅峰时刻，拉普拉斯这样写道： “假如一个智能体，在一个给定的时刻，知道了所有使世界运行的力，以及世界的每一个组成体的位置；进一步地，如果该智能体足够强大到对这些数据进行分析，它便可以用同一个方程将宇宙中最大之天体及最小之原子的运动皆囊括其内：对于这个智能体而言，没有什么是不确定的，而未来就如同过去一样，呈现于它的眼前。”拉普拉斯表达的观点叫“决定论”：世界的当前状态，精确地决定了未来发展的方式。
 
在日常生活中，决定论隐含着这样一个世界，其中，个人素质及任何给定形势或环境的性质，将直接而毫不含糊地带来精准的后果。这是一个有序的世界，其中任何事情都能被预见、计算和预测得到。但拉普拉斯的梦想要能成真，必须满足几个条件。首先，自然定律必须给定一个确切的未来，而且我们必须知道这些定律；其次，我们必须获得那些完全描述了所感兴趣的系统的数据，而且不允许出现任何不可预见的影响；最后，必须具有足够的智慧或计算能力，以根据给定的描述现在的数据，计算出定律所确定的未来是何等模样。
 
从文艺复兴晚期到维多利亚时代的这段时期中对世事所进行的研究中，许多学者对决定论都持有与拉普拉斯相同的信念。如同高尔顿一样，他们觉得人的生命历程由个人素质所严格确定，或者像奎特雷一样，他们相信社会的未来可以预计。他们常常受到牛顿物理学成功的启发，相信人类行为能被可靠地预言，就像预言其他自然现象一样。对他们而言似乎再合理不过的是，日常世界的未来就像行星轨道一般，应当能够由当前的事件状态所严格确定。
 
1960年代，一位名叫爱德华·洛伦兹（EdwardLorenz）的气象学家，试图利用当时的最新科技——一台原始计算机——在气象研究这个有限的领域内实践拉普拉斯的方案，也就是说，如果洛伦兹将他那理想化地球在某给定时刻的大气状况数据，输入那台噪声不断的计算机的话，计算机就会使用已知的气象学定律，计算和打印出一行行代表未来天气状况的数字。一天，洛伦兹决定将某个仿真的模拟时间延长些。他打算抄条近路，以运行到一半时的结果作为初始条件来开始新的仿真，而不是重复整个计算过程。他用之前打印出的仿真结果作为新仿真的初始数据，并期望计算机能再度生成先前仿真结果的剩余部分，并在此基础上给出对更遥远将来的仿真结果。但和所期待的不同，他注意到一些很奇怪的事情：新仿真中的天气演化，与旧仿真的结果完全不同。新仿真没能重复旧仿真余下的结果，反而与之严重偏离了。很快，他就意识到原因何在：在计算机内存中，数据存储精度是到小数点后6位，而在打印结果时，只保留了小数点后3位。其后果就是，他用来作为新仿真初始条件的数据，与旧仿真的对应数据之间，存在微小的差别。例如，0.293416这个值被打印出来时，就变成了0.293。
 
科学家通常假设，如果某个系统的初始条件发生很小的变化，那么系统的演化过程也同样只会发生很小的变化。不管怎样，收集天气数据的卫星在测量各种参数时，只能达到小数点后两位或三位的精度，因此，它们不能发觉像0.293416和0.293之间这样细微的差别。但洛伦兹发现，这微小的差别，却可以导致结果的巨大改变。这种现象称为“蝴蝶效应”（butterfly effect），其名称的来由，是指一只蝴蝶舞动翅膀所造成的大气状况的些微改变，也可能在之后的全球天气模式中造成巨大影响。这个观点听起来十分荒谬
 
但事实上，这种事的确会发生—回顾生命中那些重大事件的细节时，并不难发现这类看似无足轻重却导致巨大改变的随机事件。
 
世事的决定论无法满足那些拉普拉斯暗中所指的可预测性所需要的条件，原因有以下几点。首先，就目前所知，人类社会不像物理学那样，受确定而基本的定律主宰。相反，如卡尼曼和特沃斯基所一再证明的，人们的行为不仅不可预测，而且（从行为违背自身最大利益的意义上来说）还常常是非理性的；其次，即使能够如奎特雷所希望的那样，发现世事之定律，也不可能精确获知或控制生活中的局面。即跟洛伦兹一样，我们无法得到预测所需的精确数据；第三，人的事情是如此复杂，因此，即使确实了解了这些定律，获取了这些数据，能否完成必要的计算还是颇值得怀疑的。这些原因造成的结果就是，对于人类经验而言，决定论是一个很糟糕的模型。或如诺贝尔奖获得者马克思·玻恩（Max Born）所言：“相比于因果性，偶然性是一个更为基本的概念。”醉汉的脚步是随机过程的科学研究中所使用的原型。在生活中，它同样也提供了合适的模型，因为就像悬浮在布朗流体中的花粉粒那样，我们也不断地被随机事件所推动，先往这个方向，然后又朝着那个方向。如此一来，尽管在社会学数据中可以发现统计规律，但对于具体的个人而言，未来却无法预测。对于具体的成就、工作、朋友、经济状况等，我们应归功于机遇的比例，比许多人所认识到的还要大。
 
我们无法躲开那些不可预见或预测的力量，而这些随机力量以及我们相应的反应，造就了我们大部分的具体的生命之路。作为开始，我将探察一个明显与上述观点相矛盾的问题，即：如果未来果真是一团混沌而无法预测，那为什么很多事情，在事后看来却常常似乎应该能够被预见到似的？
 
1941年秋，在日本人攻击珍珠港的几个月前，东京的情报机关给在檀香山（Honolulu）的间谍发去了一个令人不安的命令。美军截获了这个命令，在一套官僚作风严重的处理程序后，情报被解密和翻译，并于10月9日送达华盛顿。消息要求檀香山的日本情报人员将珍珠港分为5个区域，并按区域报告在港舰艇，几周后，发生了另一件古怪的事情：美国监听人员再也无法跟踪到日军第一、第二舰队所有已知航母的无线电通讯，对它们的位置也一所知。然后，到12月初，位于夏威夷的第14海军辖区战斗情报单位报告，称日本人在一个月中第二次更换了舰艇呼号。这些呼号被周期性地更换。日军的习惯是每6个月或更长时间更换一次呼号，而在30天中更换两次呼号，则被视为了“大规模主动行动准备工作中的一个步骤”。这一改变使随后几天中日军航母和潜艇的行踪难以发现，从而让前面那个无线电静默的问题更令人感到困惑。两天后，发送到日本驻香港、新加坡；巴达维亚、马尼拉、华盛顿和伦敦外交与领事机构的消息被一一破解和翻译。这些消息要求外交官员立即销毁密码本，并烧掉其他所有重要的机密与秘密文件。
 
这些事后看来如此有预示性的事情，为何未能让那些与此事利益攸关的人意识到敌军的进攻正在逼近呢？
 
在一个复杂的事件链条中，每个事件的发展都带有一定的不确定性，这时，在过去与将来之间，就存在着一个根本性的不对称。自从玻尔兹曼对形成流体性质的分子过程进行统计分析以来，这个不对称性就一直是科学研究的对象。设想浮在一杯水中的染料分子。这个分子将如同布朗的花粉微粒那样，踏着醉汉的步伐前进。但即使是这种无目的性的运动，也会在某个方向上产生位移。
 
假设在某个时间点上，分子移动到了某个显眼的位置，并最终吸引了我们的注意，那正如许多人在珍珠港事件后所做的那样，我们可能会去寻找这个出乎意料的事件得以发生的原因。现在假定我们能够深挖这个分子的既往，跟踪其所有的碰撞记录，那就的确可以发现，这个或那个水分子的碰撞，推动着染料分子沿着它那曲曲折折的道路前进。换句话说，我们在事后可以清楚地解释，为什么这个染料分子的过去是以这种确定的方式发展的。但水中还有许多其他的水分子，它们也有可能与染料分子相互作用。要在实际发生之前预测染料分子的路线，需要计算所有那些具有潜在重要性的水分子的路线与相互作用，而这需要儿乎无法想象的巨量数学计算。相比于理解过去所需的那张碰撞清单，前者的计算规模和难度都要高出许多。也就是说，要在实际发生前预测染料分子的运动，几乎是不可能的，哪怕这个运动相对而言在事后更容易理解一些。
 
这个根本的不对称性，就是日常生活中存在许多其发生看来似乎十分明显但却无法预测的事情的原因。
 
上述情况对股票市场同样成立。考虑一下基金的业绩表现。下图就描绘了800支基金在1991~1995年的五年间的表现。毫无疑问，任何分析家都可以给出若干令人信服的理由，来说明图中那些领先的经理们为何会成功，垫底的经理们为何会失败，以及曲线为什么就该是这个样子。不管是否会花时间去了解这些分析的细节，没有哪个投资者会选一个在过去五年中回报率比平均水平低10%的基金，而不是一个比平均水平高10%的基金。观察过去，我们很容易构造出这样漂亮的图形和直截了当的解释，但这个充满逻辑性的图景，却不过是马后炮式的错觉，它与预测未来几乎没什么关系。例如，在第200页的图中，我将同样的800个基金再次进行了比较，其中水平轴仍然按之前五年中的排名来排列，而纵轴则表示它们在接下来五年中的表现。如果过去是未来的一个不错的指示器的话，这些基金在1991~1995年间以及1996~2000年间，其相对表现应该多少一致。也就是说，如果胜利者们（图中左方的那些基金）依旧比别人干得好，而失败者们（图中右方的那些基金）依旧干得差，那么这张图应该与上一张图差不多完全相同。但正如图中所示，将存在于过去的秩序外推到将来时，这个秩序就解体了，而新图形最终看来就如同随机噪声一般。 1991~1995年期间的最佳基金在1996~2000年间的业绩。
 
偶然性在投机以及如股权基金经理米勒这类人的成功中所扮演的角色，被人们系统性地遗漏了，而我们却总是毫无根据地相信，过去的错误必定是无知或无能的结果，并可以通过进一步学习以及提高洞察力来加以纠正。
 
正如在染料分子、天气与国际象棋的例子中那样，如果在事前跟踪事情的发展，这种必然性的感觉很快就消失无踪了。首先，除我所引用的情报之外，还有着数量巨大的无用情报，每周都有成堆的这类新消息或报告，有时带有警告意味，有时显得颇为神秘，但后来都被证明是误导或根本不重要。即使将注意力集中在事后证明具有重要性的报告上，在攻击发生前，每份这样的报告也都存在着其他的合理解释，而并不能说明针对珍珠港的奇袭正在进行中。例如，那个将珍珠港分为5个区域的要求，与其他发往驻巴拿马、温哥华、旧金山和俄勒冈州波特兰的日本情报人员的要求相类似。至于失去无线电接触也并非前所未闻，这种情况过去也常常只意味着战舰正停泊在本土港口，它们之间的通讯是利用陆上电缆来以电报进行的。更重要的是，即使相信战争的扩大迫在眉睫，许多信息却表明攻击会发生在别处——例如菲律宾群岛、马来半岛或关岛。
 
在珍珠港事件后，美国国会的7个委员会就投身于钻研之中，以求发现军方之所以忽略了所有那些表明攻击即将到来的“信号”的原因。
 
我们可以很容易地编出故事来解释过去或者对不确定的未来发展变得充满信心。我们不必因为这些做法中存在陷阱而根本不予采用。不过，我们可以努力使自己对直觉的错误产生免疫力。我们可以学会用怀疑的眼光去看待解释和预言；我们可以更注重对事件做出反应的素质，如灵活性、信心、勇气与坚毅，而非依赖于对事件发生的预测能力；我们可以更看重直接的第一印象，而非看重那些大肆张扬的当年之勇。如此就能避免在机械决定论的框架内形成判断。
 
应当预计到，复杂系统中（我将生活也归入其中）那些通常被忽略不计的次要因素，会由于偶然性而在某些时候导致重大事件的发生。
 
耶鲁大学的社会学家查尔斯·培罗（Charles Perrow）创建了一个新的意外事故理论，其理论中，培罗认识现代系统都是由数以千计的部分所组成，其中包括可能出错如人类决策者。这些组成部分以无法单独跟踪与预测的方式——就如同拉普拉斯的原子一样——相互联系在一起。但可以打赌，正如那踏着醉汉步伐行走的原子最终将到达某个位置一样，事故也将不可避免地发生。培罗这个被称为事故常态理论的学说，描述了这种情况是如何发生的，即在没有明确的原因、没有公司或政府调查组所希望找到的明显错误和无能笨蛋的情况下，事故是如何得以发生的。尽管事故常态理论研究的是事情有时必然出错的原因，但它同样能反过来解释事情有时必然成功的原因。因为在复杂过程中，不管失败了多少次，如果一直去尝试，那么最终成功的机会还是不小。
 
传统市场营销思路认为，预测消费者的偏好能带来成功。按照这种观点，管理者们最有成效的使用时间方式，应该是去研究到底是什么东西让斯蒂芬·金（Stephen King）、麦当娜或布鲁斯·威利斯（Bruce Willis）这类人的粉丝们如此着迷。他们对过去进行了研究，并且——如我所说的——没费什么力气就找出了成功的原因，不论他们希望解释的成功到底是什么东西。然后，他们希望能复制这些成功。这就是市场的决定论观点，在这种观点下，成功主要取决于某个人或产品的内在素质。但我们还能以另一种方式——一种非决定论的方式——来看待成功。在后一种观点下，世界上还有着许多高质量但不为人知的书籍、歌手、演员，而真正能让这一个或那一个冒出头来的，则很大程度上是随机性与各种次要因素合的结果，也就是运气。
 
多亏了因特网，这个观点已经埽到了验证，进行验证的研究者们将注意力放在了销售额主要来自因特网的音乐市场。为进行研究，他们雇用了14341名参与者，让他们听一些他们从未听说过的乐队所演唱的48首歌曲，对它们打分，并且——如果愿意的话——下载这些歌曲。有些参与者能够看到这些歌曲的流行度数据——即在其他参与者中，有多少人下载了这些歌曲。这些参与者被分到8个相互分离的“世界”中，并且只能看到同一世界中的参与者下载歌曲的情况。每个乐队在各个世界中的初始下载量都为0，之后每个世界就独立地演变。此外还有一个第九组，其中的参与者看不到任何数据。研究者们用这最后一组隔绝的听众们所给出的歌曲流行度，来定义每首歌的“固有质量”——即在没有外界影响的情况下，这些歌曲所具有的吸引力。
 
如果决定论的世界观是正确的话，在前8个世界中占优的，应该都是同一些歌曲，而且这8个世界中的歌曲排行，应该与第九组的孤立听众们所给出的固有质量相一致。但研究者们所发现的却恰好相反：各首歌曲在不同世界中的受欢迎程度天差地别，而固有质量相近的不同歌曲，其受欢迎程度也大相径庭。
 
在这个实验中，如果这首或那首歌曲，偶然地在早期获得了下载量优势，那么这首歌曲颇受欢迎的表象，就会进一步影响后来的购买者。在这个例子中，小的随机影响产生了滚雪球效应，使歌曲的未来天差地别。我们又一次看到了蝴蝶效应。
 
通过生活中细致入微的观察，同样能发现，在许多重大事件中，如果没有那些偶遇的人、偶然到来的工作机会以及各种各样小因素的随机汇合，结果可能会大相径庭
 
显然，以与其财富成比例的方式来赋予人们才智，很可能是个错误。我们无法看到某人的潜能，而只能看到其结果，因此，我们常常认为结果必然反映能力，并因而对这个人形成错误的判断。生活的事故常态理论证明，行动和收获之间的联系虽然并非随机，但随机影响却与我们本身的素质及行动同等重要。
 
许多人情感上都不愿接受随机影响非常重要的这个看法，哪怕他们从理智上能够理解事实的确就是如此。如果人们低估了机遇在那些巨头的职业生涯中所扮演的角色，那对于机遇在最失败者的生活中所扮演的角色，他们是否同样没有给予足够重视呢？
 
我们也许不觉得自己会根据人们的收入或成功的外在表现来衡量他们，但即使知道一个人的薪水完全由随机所确定，还是有许多人无法避免直觉地认为薪水与价值相关。人们是否倾向于认为，那些不成功或正在承受痛苦的人，确实是活该如此
 
我们看漏了随机性在生活中的影响，因为在评价这个世界时，我们倾向于看到自己所希望看到的东西。我们实际是通过成功的程度来定义才能的高低，然后再通过才能与成功之间的相关性来进一步强化这种因果关系。
 
能力并不保证定能获得成就，而成就也并非与能力成比例。因此，重要之处在于不要忘记这个成功方程式中的另一项——偶然性所扮演的角色。
 
我所学到的，首先就是一直向前，因为最好的消息就是，既然偶然性确实扮演了某个角色，那通往成功的要素之一就在我们掌握之中了：我们上垒击球的次数，我们获得机会的次数，我们把握机会的次数。因为即使是一枚更容易掷出失败结果的硬币，有时也会掷出成功。或者如IBM先驱托马斯·华生（Thomas Watson）所说：“想要成功，就把你的失败速度加倍。”
 
我们通过结果来评判人和动机，我们希望事情的发生乃是由于良好且可以理解的原因。但我们所看到的清晰的必然性，通常不过是错觉罢了。我相信，在面对着不确定性时，我们能够重新组织我们的思维方式。
 
我们可以提高决策技巧，并克服某些能导致不当判断与选择的偏见。我们应该不以成败论英雄地了解他人的能力与各种情况，并学会通过所有可能结果的分布而非实际所得的结果，来判断决策的优劣。
 
我们应当看到我们所得的好运，并对此心怀感恩，进而认识到随机事件在成功中所占的分量。最重要的是，它教会了我去感恩，庆幸没有碰到坏运气，没有碰到那些可能击倒我们的事，没有经历疾病、战争、饥荒，以及那些没有——或者说尚且没有——落到我们头上的意外。
==========