初中数学获奖课例及点评
《初中数学获奖课例及点评》
黄家礼主编
现代教育出版社
勾股定理的逆定理
执教：全国一等奖获得者  华英姿
    华英姿，上海市建平中学毕业后考入华东师大数学系，获本科文凭，学士学位。现为上海某中学数学教师。曾获：
    南汇区初中青年数学教师教学交流与评选一等奖；
    上海市中小学首届“君远杯”青年教师教学比赛一等奖；
    上海市初中青年数学教师教学交流与评选一等奖；
    全国初中青年数学教师优秀课观摩与评选活动一等奖。
师训读本
课例点评
核心期刊
    华英姿执教的《勾股定理的逆定理》一课及点评后被上海市《2006师训读本》、《初中数学课例点评》收录，也在中等教育核心期刊《中学数学教学参考》上发表
课堂实录
勾股定理的逆定理
教学目标
1. 能应用勾股定理的逆定理判定一个三角形是否是直角三角形；
2. 会运用勾股定理的逆定理解决有关证明与计算问题；
3. 通过勾股定理逆定理的证明的探究，体验、感悟知识的生成和发生过程，体会从特殊到一般的认识规律与数形结合的思想；
4. 通过参与课堂活动，感受探索、合作的乐趣，并从中获得成功的体验. 
教学重点与难点
教学重点：勾股定理的逆定理的应用.
教学难点：勾股定理的逆定理的证明.
教学过程
1
提出猜想，证明猜想
课
堂
实
录
点击边框调出视频工具条   应用训练，巩固新知
2
点击边框调出视频工具条   课
堂
实
录
3
归纳小结，拓展提高
课
堂
实
录
点击边框调出视频工具条   勾股定理的逆定理
教学设计
勾股定理的逆定理
教学设计思路
《勾股定理的逆定理》 的教学设计思路
  华英姿
    勾股定理是欧氏几何中最著名的定理之一，是数形结合完美的典范，它有着悠久的历史，在数学与人类的实践活动中有着极其广泛的应用.勾股定理的逆定理是其中的一部分重要内容。勾股定理及其逆定理的发现、证明和应用蕴涵着丰富的文化价值.本课是勾股定理的逆定理的教学，它是在学生掌握了勾股定理的基础上，继续学习与勾股定理有关的内容.
一．目标分析
    本节课的教学目标如下：
    掌握勾股定理的逆定理，会用它判定一个三角形是否是直角三角形；会运用勾股定理的逆定理解决有关证明与计算问题；通过勾股定理逆定理的证明的探究，体验、感悟知识的生成和发生过程，体会从特殊到一般的认识规律与数形结合的思想；通过参与课堂活动，感受探索、合作的乐趣，并从中获得成功的体验.
    上述教学目标，依据《上海市中小学数学课程标准》，与章节目标对应，体现了三个维度，符合初二学生的认知发展水平和心理特征。具有针对性、层次性和可操作性.
二．重点难点分析
教学重点：勾股定理的逆定理的应用.
教学难点：勾股定理的逆定理的证明.
    教学重点、难点是根据课程标准、教材、学生实际确定的.教材中这一节的大标题是几何计算，所以把“应用”作为重点；逆定理的证明采用的是“构造法”，在上海版整个初中教材中只出现了这一次，怎么想到这个方法是这节课的一个难点.
三．学生分析
    在知识掌握上，学生已具备直角三角形、勾股定理内容的有关知识，积累了一定观察、
操作等活动经验，具有简单的说理及初步推理能力，因此本课在引入部分设计的探究活动，学生经努力是能做到的.
    在学习心理上，抓住学生对游戏感兴趣的特点，在课程最后一个环节，给学生创造一个兴奋点，使本节课的气氛再次达到高潮.通过师生之间、生生之间的融洽合作，使学习活动变得轻松、有趣，同时新知得到巩固，能力得到训练，认识得以升华.
    在思维角度上，“操作+思考”的方式符合八年级学生认知水平，适应其思维发展规律及心理特征。他们求知欲强，想象力丰富，乐于参与操作活动，有充分展示及表现的愿望.但也存在耐挫能力不强、注意力易分散的不足.因此，在学法上，既要充分发挥学生在教学中的主体作用，采取让学生自己观察、大胆猜想、严密论证，又要适时发挥教师的指导作用.
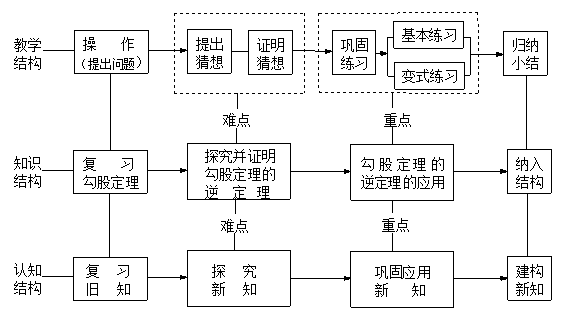
四．整体结构设计
    通过上面的分析，最终形成对本节课的整体结构设计如下：
勾股定理的逆定理
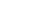
教学过程设计简述